Building strong number sense is crucial to ensure success in math. In grades K-3, one key area that sets the foundation for more complex mathematical concepts is understanding how numbers can be composed and decomposed.

This skill  prepares students for operations like addition and subtraction and fosters flexible thinking about numbers. In this blog, we’ll explore how learning trajectories guide students through these concepts. I’ll also share practical strategies for teaching composing and decomposing numbers in early elementary math, and we’ll see how Structures of Equality (SoE) help develop this skill.

What are learning trajectories in early math?

A learning trajectory is the path students follow as they move from simple to more complex mathematical understanding. These trajectories help teachers understand how to guide instruction in a developmentally appropriate way.

Research in early math education, such as the work by Dr. Julie Sarama and Dr. Douglas Clements, shows that understanding learning trajectories can build deeper understanding and stronger math skills over time.

“Teachers who understand learning trajectories are more effective and efficient and engage children in mathematics joyfully. Through planned teaching and also by encouraging informal, incidental math, teachers help children learn at an appropriate and deep level.” (Clements, D. H., & Sarama, J. (rev 2023). Learning trajectories in early mathematics: Sequences of acquisition and teaching)

One strand of these trajectories is composing and decomposing numbers. These skills – putting numbers together to form larger ones, and breaking them apart into smaller components – help children understand how numbers work. This helps create flexibility with number sense and prepares students for more advanced math concepts like place value, addition, and subtraction.

The basics of composing and decomposing numbers

Composing Numbers

Composing numbers is the process of putting together, or combining, numbers to form a total. For example, students might learn that 5 + 3 equals 8, which helps them understand that numbers can be “built” from parts. This teaches them the concept of part-whole relationships, that every number is composed of other numbers.

Students begin to see there are multiple ways to form the same number. For instance, 7 can be made by joining 5 + 2, 4 + 3, or 6 + 1. As children practice this, they develop an understanding that numbers are not fixed but are flexible and can be manipulated in different ways. They also solidify essential understandings like conservation of number, quantity, value, and magnitude.

Decomposing Numbers

Decomposing numbers is breaking down a total into parts. For example, 10 can be broken down into 6 and 4, or 7 and 3. Helping students internalize this idea develops their mental math strategies, freeing up valuable space when they grapple with more complex ideas. Decomposing helps students see how numbers relate to one another, allowing them to “take apart” numbers to more easily access mathematical problems and ideas.

It’s also important to build the understanding of how composing and decomposing are related concepts.

Learning progression for composing and decomposing in K-3

As children progress through kindergarten to third grade, their understanding of composing and decomposing numbers evolves. Here’s a look at how these skills develop across the early grades:

Kindergarten

In kindergarten, children explore numbers up to 10 and begin to work with teen numbers. They practice composing and decomposing numbers using concrete objects like counters, fingers, or simple drawings. For example, they might be asked, “How many ways can you make 5?” They’ll experiment with different combinations like 4 + 1 or 3 + 2, using objects to see how parts make a whole.

1st grade

By first grade, students work with decomposing numbers up to 99, and they start applying their knowledge to addition and subtraction problems within 20. They begin to see numbers as more flexible and start breaking numbers apart more intentionally. A typical activity might be “Show different ways to make 10,” such as 9 + 1 or 7 + 3. This lays the groundwork for understanding more complex addition and subtraction concepts.

2nd grade

Second graders move on to composing and decomposing larger numbers, especially focusing on place value. They work with numbers up to 999 and begin decomposing numbers up to 100 into tens and ones and thinking flexibly about place value. This skill is crucial for understanding two-digit and three-digit addition and subtraction.

3rd grade

By third grade, students apply these skills to multiplication and division. They begin thinking about groups of numbers and how they can be composed and decomposed in terms of factors and equal groups. For example, 24 can be decomposed into 4 groups of 6 or 6 groups of 4. This early experience with number flexibility supports multiplication, division, and algebraic thinking later on.

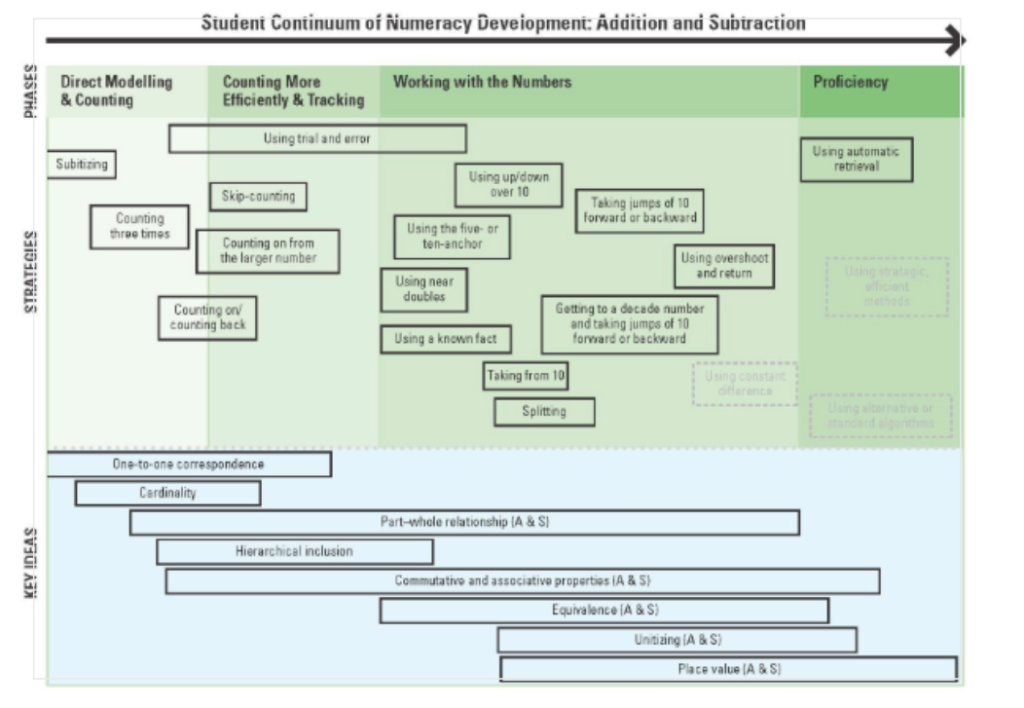
This continuum from Thinking Mathematically shows how the idea of part-whole relationships plays a role from the counting phase all the way up to the automatic retrieval phase.

With a clearer understanding of how children develop these skills across grade levels, let’s explore some effective strategies for teaching composing and decomposing numbers.

Strategies to teach composing and decomposing numbers

Use concrete materials

One of the most effective ways to teach composing and decomposing numbers is the use of manipulatives. Objects like base-ten blocks, counters, and snap cubes allow students to physically build and break apart numbers, making abstract concepts more tangible.

Visual representations

Encouraging children to draw number bonds, part-whole diagrams, or use number paths and number lines can help them visualize the relationships between numbers. These representations offer a bridge between concrete materials and more abstract math concepts, showing how numbers can be broken apart and put back together.

In Structures of Equality (SoE), both Parts Equal Total and Repeated Equal Groups are part-whole diagrams. Each representation models a number story in which a total is being composed into parts or where parts are being composed to form a total. 

When modeling stories that represent comparison situations, the line of equality helps students understand how to decompose the longer bar into the part that is equal to the smaller value and the “more”.

Number stories

Find real-life scenarios where children can apply composing and decomposing. For example, ask them how they can split materials, like crayons, between the table groups. These types of problems make math relevant and encourage deeper thinking.

Fostering a growth mindset in math

When teaching composing and decomposing numbers, it’s important to foster a growth mindset. Flexible thinking is key to math proficiency. Encourage children to explore different strategies and approaches, and emphasize that making mistakes is a natural part of learning. Creating a positive and supportive learning environment can help children feel confident in their math abilities.

Conclusion

Composing and decomposing numbers are essential skills in developing number sense, and they serve as the foundation for much of the math learning that follows. By understanding how these concepts fit into learning trajectories, we can help all students build strong mathematical foundations.