September 25, 2024
Place value and number sense go hand in hand. When students struggle with concepts like decimals, fractions, or even basic operations, the underlying issue is often a lack of true understanding around place value – the foundation of our number system. Helping students understand place value at the conceptual level starts as early as kindergarten.
What is place value?
Place value is the value of each digit in a number based on its position. And while that sounds simple, it’s really pretty complex. To understand place value, you need to understand the relationship between the digits based on their position.
Our number system is a base ten system. “Simply put, base-10 is the way we assign place value to numerals.” (Deb Russell, Thoughtco) We use ten digits, 0-9, to represent the values. We then assign a place value based on the position of the digit in a given number.
Place value examples
A common way to model place value is through a tens and ones chart. For example, the number 53 could be thought of as 5 tens and 3 ones. While this is true, it’s just the beginning.
The value of the 5 in 53 is really 50. A student with deep understanding can think of 53 as 50 and 3. They can also think of it as 53 ones, or 40 and 13.

Why do some students struggle with place value? The problem occurs when students think of place value as a procedure, as putting a digit in its place. To combat this, we have to teach students to think flexibly about numbers and their forms.
How do you teach place value to build number sense?
Then
Traditionally, we taught place value by giving students objects to group into tens and ones, usually starting in first grade when numbers exceed nineteen. In kindergarten, we might have counted days or celebrated the 100th day of school, often in a procedural manner.
Now
Building flexible thinking around place value starts the first time students work with numbers past nine. We need to make a really big deal about something incredibly important happening with our numbers when we get to ten. We’ve run out of digits!
It might sound something like this. “Oh no! We have 10 cubes but I only have a place for one digit and the number ten is written with two digits. What should we do? Does anyone know how to write ten?
You can make a big deal about trying to squeeze the 1 and 0 together into one place where they don’t fit. “I know. Let’s give them each their own place. I have ten cubes. But I could also say I have one group of ten cubes. Here’s how I would write it. 1 to show one group of ten and 0 to show no ones leftover.”
You can make a big deal out of this with every teen number. Then, every time you get to a new ten.. You don’t write 20 as 19-1 or 10-10. You now have 1 group of 20 and 0 ones, so you write it as 20.
This is where place value gets really fun, and where we can have a huge impact on kids’ understanding of the number system. When we get to 20, we can start talking about all the different forms of the number. Yes, it’s 20 ones. But it’s also 2 tens and 0 ones. Or 1 ten and 10 ones.
Students now begin to think flexibly about the values of those numbers. By the time they reach double-digit addition and subtraction, they’re used to thinking about numbers flexibly, reducing confusion around regrouping.
Here’s an activity you might like to try. You can put a number on the board and ask kids to think of all the ways they could represent that number in all its forms. It will likely end up looking something like this at first:
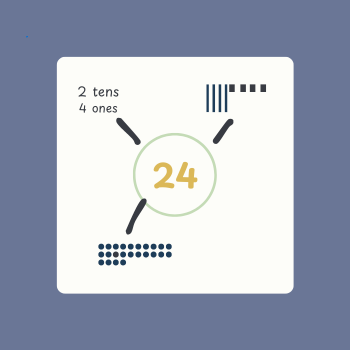
As you practice, their thinking will start to get more sophisticated and you’ll begin to get responses like this:
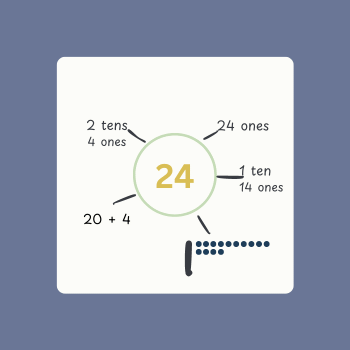
By engaging in this activity, which I would recommend as a daily or weekly routine, you’re making connections between concrete, representational, and abstract ideas.
Conclusion
Understanding place value is critical for developing number sense. By starting with smaller values in our work with whole numbers, we create the conditions for students to grapple with complicated numbers later on. Ideas like the translation from fraction to mixed number makes sense because we’ve taught them how to think about the varying forms the value of a number can have.