May 1, 2024
Introduction: What is CRA?
CRA stands for Concrete-Representational-Abstract. Initially, the CRA framework was conceived as a linear progression with students moving from concrete models to abstract ideas. As we’ve learned more about the CRA framework in early math, this thinking has evolved. Rather than a series of steps or each phase taught in isolation, we’ve learned the benefits of integrating them within the same concept or problem. First, we’ll define each phase. Then we’ll explore what it looks like in action.
Defining Each Phase
Concrete: Hands-On Exploration
Ideas are explored through hands-on exploration and concrete objects. This might include manipulatives such as fraction bars, counting bears, or 3D models of shapes.
Representational: Visual Representation
Students represent concrete ideas visually. This could look like drawing 3 apples and 2 apples to solve 3 + 2 or drawing 5 circles with 6 dots in each circle to solve 5 x 6. For examples with bar models and number lines, I love this vlog by Christina Tondevold, How to Use Representation in the CRA Method.
Abstract: Symbolic Representation
At this stage, ideas are represented with symbols, often numerically. An example would be 8 + 4 = 12.
At any point in mathematics, students might need to move between the phases to develop both conceptual and procedural understanding.
Why is it important to use the CRA framework in early math?
Building Strong Foundations
Developing proficient mathematicians starts with a strong number sense foundation. As educators, we sometimes mistake fast for smart or accurate answers for understanding.
We’ve all had that student who’s flown under our radar. Picture it: a kindergartener who’s excited because they can count past 100 and already knows some multiplication. They fly through the work you provide. But, when you ask them to explain, they’re stumped. They don’t know how they got their solution, they just did.
Now let’s consider a 2nd grader. They can solve every addition and subtraction problem using tools like base ten blocks and can easily explain ideas like regrouping. They’re flexible in their thinking. But give them a worksheet with problems and they can’t translate the concept to practice.
While these cases are at opposite ends of the continuum, the CRA framework can help fill in the gaps for both of these students. Shelley Gray states “When you teach a math lesson, make it your goal to incorporate concrete, representational, and abstract into the same lesson. This way you can be certain that you are differentiating for all your students, regardless of where they are in their understanding.”
Making Connections
To make sense of mathematics, students need to make connections between the concrete, representational, and abstract. This is where the magic happens.
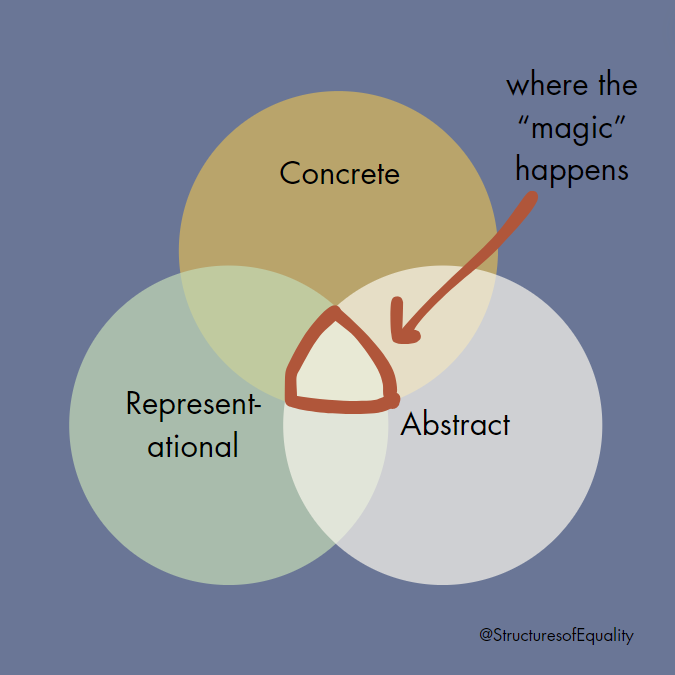
CRA in action: examples
Now that we understand the significance of the CRA framework, let’s look at a few real-life examples.
Addition
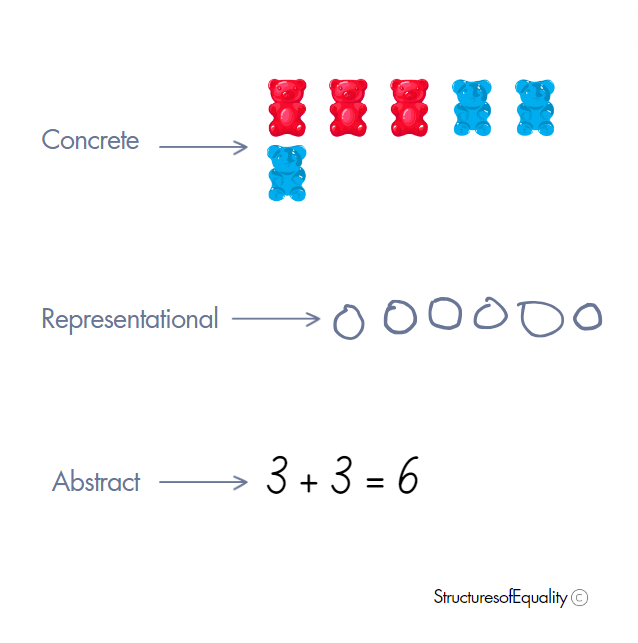
Here’s what solutions might look like in a lesson where students are figuring out the value of 3 + 3.
Think back to the kindergartener we talked about earlier. Given an option to show their work any way they want, they’d likely choose abstract. They might know that 3 + 3 has the same value as 6 because they’ve memorized it. If they see another student, or you as the teacher, model it concretely, they can make the connection and bridge that gap. In the same lesson, the student who has to draw a picture to solve can see the equation that represents their visualization.
As students progress in their mathematical thinking and are exposed to more challenging ideas, such as break apart to make ten, the CRA framework remains essential. If we don’t teach students how to reason and critically think at the foundational level, we leave them ill-equipped to make sense of math as they move into harder concepts.
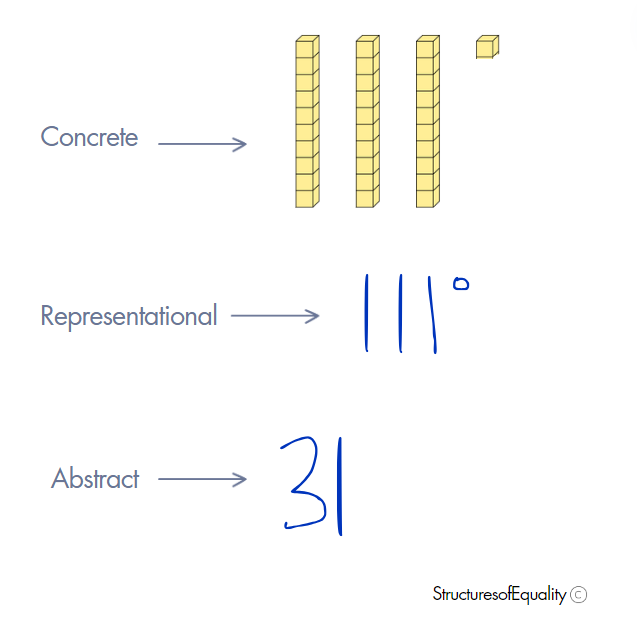
Place Value
Place value understanding is critical if we want students to be adept with our base-ten number system. I’ve been in many classrooms where students can tell me that 31 has 3 tens and 1 one but aren’t able to explain what that means. They don’t understand the idea that 31 can also be 31 ones, or 2 tens and 11 ones.
This shows up later as confusion when using the standard algorithm to solve multi-digit addition. When students actively engage in place value at the concrete, representational, and abstract levels, we are providing them with the conceptual understanding they need to successfully perform procedural functions in later math.
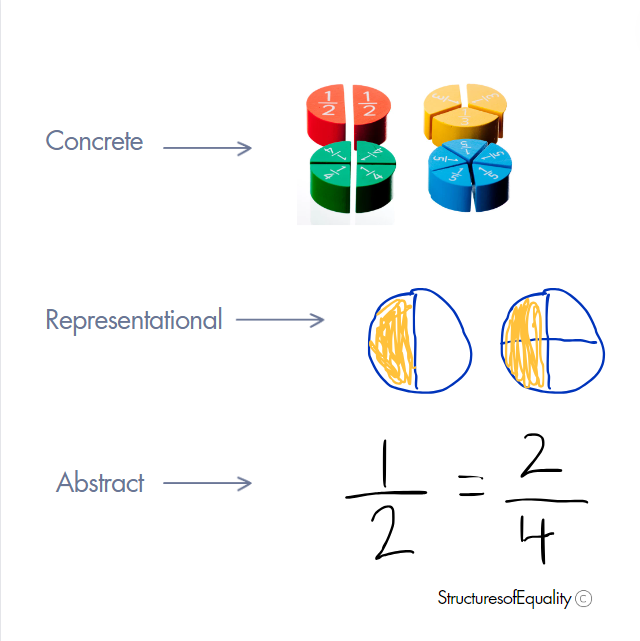
Fractions
Fractions tend to be a hard concept for students in general. They’ve only worked with whole numbers up to this point and think of fractions as an entirely different idea. If students don’t conceptually understand the idea of fractions, they struggle to understand that fractions are numbers with a value (not some foreign concept).
Students who are exposed to equivalent fractions at the abstract level may learn procedures such as multiplying the numerator and denominator by the same number to create an equivalent fraction. What they fail to see, unless they’ve worked with fractions at the concrete and representational levels, is that ½ and 2/4 can be different symbolic ways to represent the same numeric value. They also won’t have exposure to the idea that ½ and 2/4 might not have the same value. ½ of 2 pizzas is a very different amount than 2/4 of 3 pizzas.
I bet you can see why multiplication of fractions can be such a challenge if students haven’t worked within a CRA framework!
Conclusion: Looking Ahead
We’ve only touched the tip of the iceberg. I’ll delve into CRA more deeply in the future. Regardless of the concept or skill you’re teaching, exposing students to all approaches within this framework helps them develop a deeper understanding of mathematics. Next time, we’ll see exactly how CRA works within Structures of Equality. Don’t want to miss it? Make sure you’re subscribed to my email list!