October 2, 2024
What does the number of marbles in a jar have to do with mathematical proficiency? While this is a common association, teaching estimation is more complex.
If you’ve ever asked little kids to guess how many of something, you’ve probably gotten a huge variety of responses. Most of them probably aren’t even close! That’s because accuracy with estimation increases with age and experience.
What does the number of marbles in a jar have to do with mathematical proficiency? While this is a common association, teaching estimation is more complex.
If you’ve ever asked little kids to guess how many of something, you’ve probably gotten a huge variety of responses. Most of them probably aren’t even close! That’s because accuracy with estimation increases with age and experience.
At around 2nd grade, kids become more skillful with estimation tasks. Siegler and Booth, curious about the relationship between number-line estimation and math achievement, conducted a study on kindergarten through 2nd graders.
The interesting find? “Accuracy of estimation on the number-line task correlated with math achievement at all three grade levels.”
That seems pretty significant and it’s what inspired today’s topic: Why is teaching estimation important?
We’ll cover:
- What is estimating?
- Estimation in everyday life
- Estimation and mathematical proficiency
- Resources and ideas for your classroom
Estimating is a bit more complicated than guessing the number of marbles in a jar or candies in a bowl. There are many different types of estimation that go way beyond quantity. This idea really resonated with me:
What is estimating?
“Estimation… encourages children to have a good understanding of the magnitude of numbers rather than overly relying on mathematical procedures to achieve an answer.” (Bartlet, Third Space Learning)
It’s about making educated guesses and relevant approximations in all domains from measurement to operations and algebraic thinking. Estimation isn’t explicitly taught until 2nd grade (if you follow the Common Core standards). I always wondered why, until I read the study I mentioned earlier.
Since it’s a key part of number sense, there’s a lot we can, and should, do to lay the foundation from an early age.
Estimation in everyday life
As adults, we use estimation every day. We use number sense strategies to figure out things like our approximate grocery bill or how many minutes it will take to complete a task.
If you’re an early childhood teacher or a caregiver (or you work with a student who struggles with estimation), here are a few ways you can incorporate it into daily activities:
Pose questions like:
- About how many steps do you think it will take us to get to the playground?
- Around how long do you think you can hold a handstand underwater?
- I wonder about how many Pokemon cards fit on each page. What do you think?
- How far do you think we can throw the paper airplane?
Notice the intentional word use. “About”, “around”, “wonder”, and “think” help build the language of estimating. After engaging in the activities, you can continue to build language around the concepts of confirming or revising estimates.
- Why do you think that?
- Wow, we were really close! How far do you think it is to…?
- Boy, we were way off. We guessed a lot higher than the amount it actually took.
This also helps make the relationships between estimates and actual values evident.
Estimating and mathematical proficiency
The Standards for Mathematical Practice were developed to help define what students need to be able to do to be proficient mathematicians. When it comes to estimation, students engage heavily in Practice Standards 1 & 2.
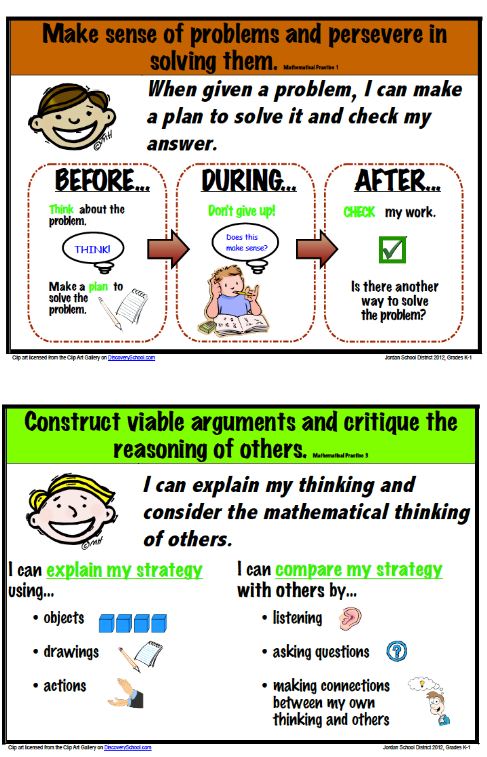
Standard 1: Make sense of problems and persevere in solving them
Have you ever asked your students if their answer makes sense only to get a blank stare? Or to have them nod yes, even though their response is wildly inaccurate?
This is likely because they follow a rote procedure without conceptual understanding. It happens with number stories all the time. Kids plug and chug by picking the numbers out of a story, choosing a random operation, and “solving”.
To help fix this, we have to teach kids how to slow down. An easy way to do this? Estimation!
Before students tackle a problem, ask them what they think the answer might be. This is a skill they have to develop so it takes a lot of modeling, practice, and time before they make educated guesses for their estimates.
Then, after solving, ask them to refer back to their estimate to see if their answer makes sense. For example, if they’re adding 23 + 29, a student might estimate 50 because they rounded and noticed 20 + 30 equals 50. That means the solution should be close to that.
Now, let’s say the student solves the problem and makes a classic mistake. Due to a lack of understanding around place value, they forgot to regroup. This could show up a couple different ways.
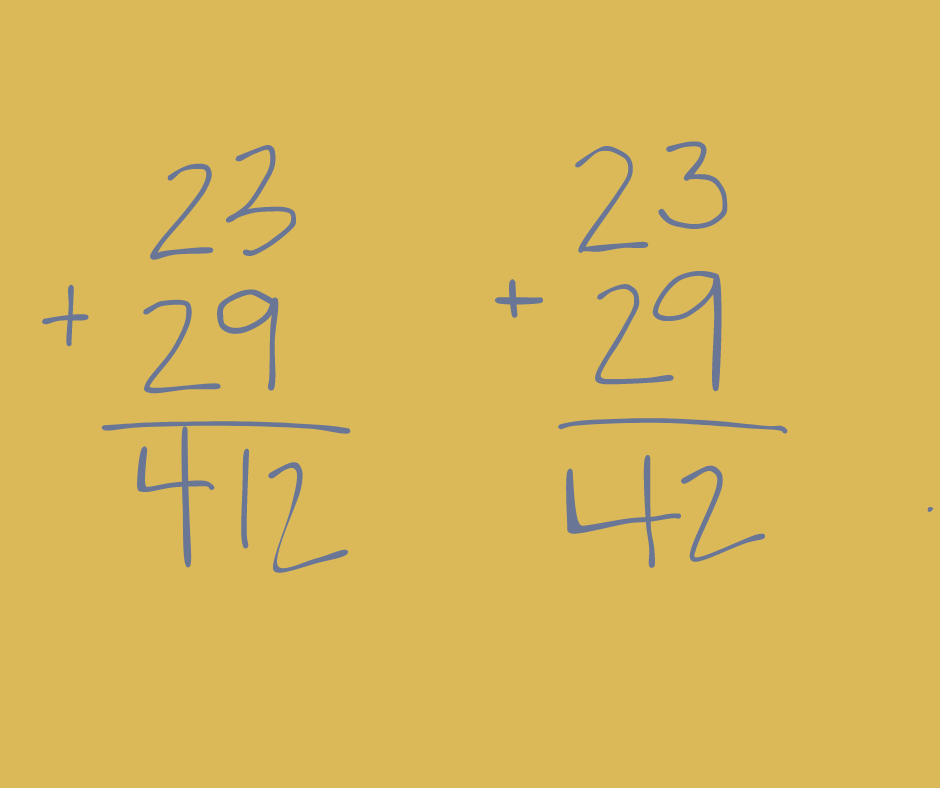
In the first example, they get a sum of 412. That’s way off base. Their estimate will help them.
The second example is trickier. They get a sum of 42. When you ask, “does your answer make sense in relation to your estimate?”, they’ll notice it doesn’t. You can then say something like, “Hmmm. You’re right! It doesn’t make sense. I wonder if you can find the mistake. I’ll come back and check with you in a few minutes.”
Now, let’s say you have a student estimate “more than 40”. They likely used front end estimation. They noticed 20 + 20 equals 40. Since both values are greater than 40, the solution must be too.
That’s actually strategic thinking. That kind of estimation makes sense in some situations. This brings us to Practice Standard 2.
Standard 2: Reason abstractly and quantitatively
As a teacher, this is your opportunity to engage in discussion. In this situation mentioned above, you might ask questions such as:
- I noticed some people rounded for their estimates and got 50 which was close to the solution. Why do you think rounding makes more sense in this situation than front end estimation?
It’s important that students understand different situations call for different types of estimation. Let’s look at an example of front end estimation as an efficient strategy.
In the case of decimals, students will get a reasonable estimate that makes sense. For example, when solving 5.9 + 16.234, a student could say something like: 5 + 16 is 21 so my solution would be close to that.
Then, when making the classic mistake of not using proper place values, they’d instantly notice their error.
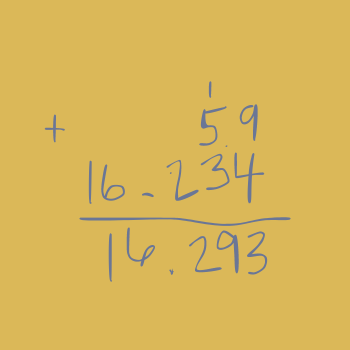
When you ask, “Does that make sense with your estimate?”, they’d notice it doesn’t and quickly be able to catch their own mistake.
Adding in the small step of estimating before solving develops number sense by helping students focus on ideas such as magnitude and place value.
Resources and ideas for your classroom
By now, you’ve seen the benefits of teaching estimation. But you may still be wondering – how do you teach students to estimate?
Here are a few of my favorite resources:
- This lesson is a fun and relevant way to introduce estimation in kindergarten. I especially like the literacy connection!
- Estimation 180 offers over 200 days of estimation activities for grades 4-8.
- There are loads of K-12 activities on Esti-Mysteries. He comes out with new ones every year!
Conclusion
Teaching estimation is a critical part of helping our students build number sense. Because of limited time and lots of demands, it’s often one strategy that gets overlooked. Hopefully, you’ve found new, easier ways you can effectively incorporate estimation into your instruction.