October 30, 2024
I love tips and tricks that make my life easier. But when it comes to math, relying on shortcuts can be more harmful than helpful. Sure, they might save a few seconds now, but in the long run, they rob students of the critical thinking skills they need to truly understand math. And math, unlike Halloween or magic, isn’t about tricks – it’s about comprehension.
Why math tricks are problematic
When I was in school, math was about memorization and rote procedures. It was about being quick. Since then, our thinking around math has evolved quite a bit. We know that proficient mathematicians make sense of math. They’re critical thinkers and problem solvers. While tips and tricks may seem efficient, they can be detrimental in the long run.
The popular ‘9s trick’ and its flaws
I bet you’ve come across the 9s trick for multiplication at some point. You use your hand to find the product of a number with a factor of 9. It works like this: Let’s say you’re trying to find the solution to 9 x 5. You hold up 10 fingers, count 1,2,3,4,5, and put your 5th finger down. Now you have 4 on one side and 5 on the other, which is also your product, 45.
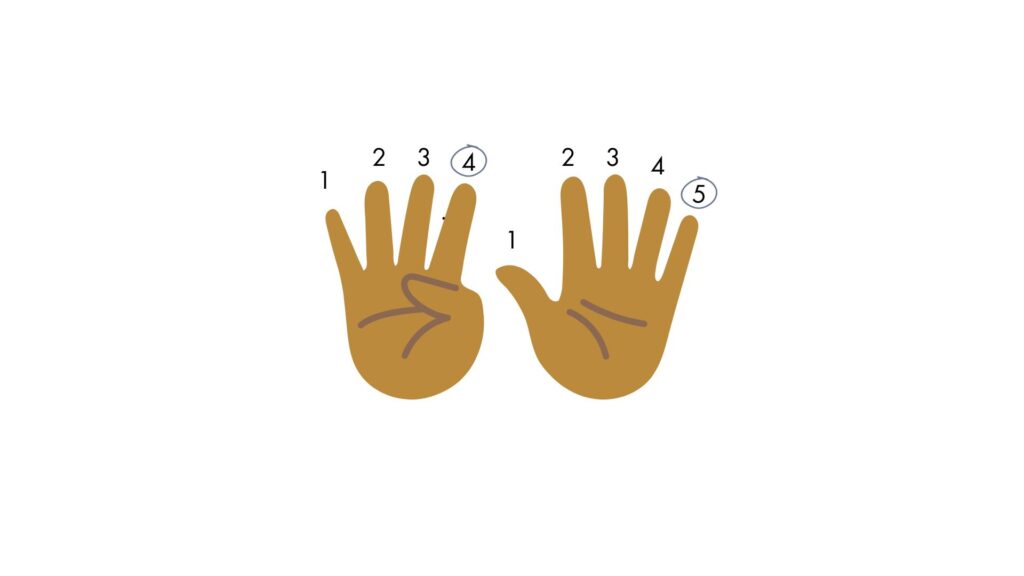
I’ll admit, it’s pretty cool. The problem? “A significant amount of maths in KS2 and beyond depends on the ability to think and reason multiplicatively.” (NCETM)
When kids struggle with fractions, proportions, trigonometry… it can often be traced back to challenges with thinking multiplicatively.
There must be a balance between conceptual and procedural repetitions. If students can’t explain why a tip or trick works, they shouldn’t use it.
So how should we teach multiplication and multiplicative thinking?
Developing multiplicative thinking
Let’s revisit the factor of 9. We know that 9 is one less than 10. That means 9 groups is 1 group less than 10 groups. Since we have a base-ten number system, we spent time helping students understand how to think in groups of ten and what our place value system really means.
With this knowledge, we can make explicit connections to develop multiplicative thinking. If I have 9 x 5, I can use what I know about 10 x 5 to help me figure out the product.
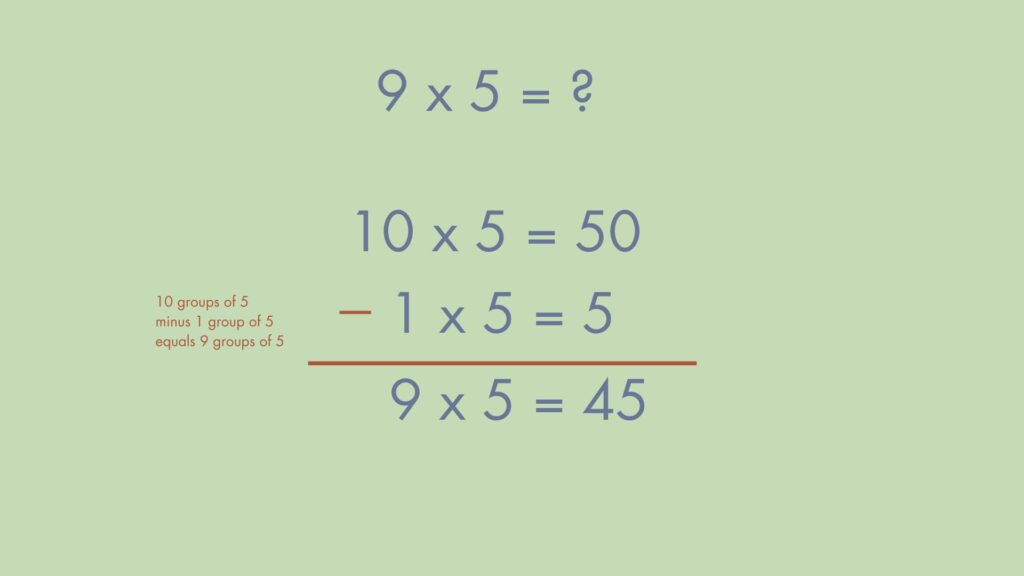
Some argue this is exceedingly complex and there are too many unnecessary steps. I argue this. What happens when a student is later faced with 9 x 52? You don’t have 52 fingers. But you can quickly figure out that 10 x 52 is 520, so we need one group of 52 less.
Instead of getting frustrated and giving up, students are empowered to make sense of what’s happening.
This frustration also shows up when students are working with word problems. And that’s another place kids look for shortcuts or tricks to help them, like using keywords or procedures such as CUBES.
A better way to teach word problems
When I work with teachers, I always ask them their biggest challenge with teaching word problems. The most common answer? Their students don’t understand what the problem is asking – they can’t comprehend the problem. 59 of the 87 teachers who answered this question in my Facebook group said the same thing. Their kids pluck numbers instead of making sense of what’s happening in the story.
That’s why Structures of Equality (SoE) is about making sense of math stories.
Let’s look at a sample story similar to one that often confuses students.
Lucy has 16 apples. Julie has 9 apples. How many more apples does Julie have than Lucy?
Solved with CUBES and a focus on keywords, a student’s work might look like this:

Because they relied on tips and tricks, they didn’t have to make sense of the story. They plucked the numbers, chose the “correct” operation, and solved.
A student who understands what’s occurring in the story could use a Compare structure to represent it like this:
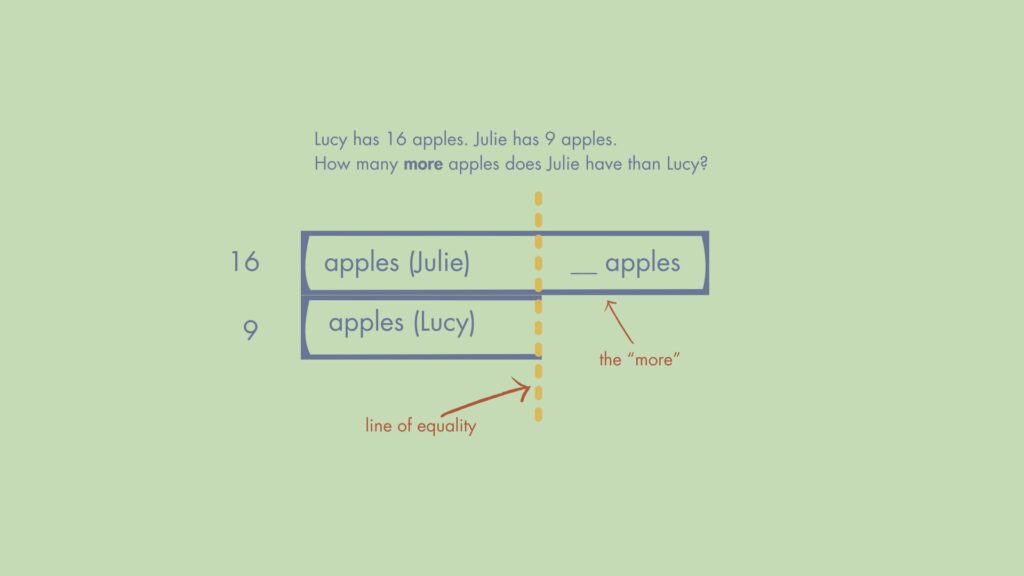
This demonstrates comprehension of what’s happening in the story – the skill most teachers say their students lack. It’s a visual model of the situation exactly as it’s occurring in the story.
Is it quicker or easier? No. Will it help students become proficient mathematicians? Yes.
Conclusion
In math, there’s no shortcut to true understanding. While tricks and tips may offer temporary relief, they undermine students’ ability to develop critical thinking and problem-solving skills. By emphasizing conceptual understanding, particularly through methods like multiplicative thinking and Structures of Equality, we can empower students to make sense of math, not just memorize it. Ultimately, the goal is not quick solutions but lasting comprehension that equips students to tackle more complex mathematical challenges with confidence.
Did you find this helpful? I’d love for you to join my Structures of Equality (SoE) communities.