What is zero anyway? And do you really have to teach it? 

Zero, represented by the numeral 0, signifies the absence of a value. This concept changed mathematics and our understanding of numbers. While it may seem like an abstract idea, it is very much a real number and does need to be taught.

If you’re an elementary math teacher, or a caregiver, you probably haven’t had to think about the number system since you were in school. And if you’re like most – it’s out of sight, out of mind.. Let’s start there.

For our purposes, we’re only going to explore natural and whole numbers today. If you want to dive into the rest of it, Neha Khandelwal wrote a thorough explanation you can find here, which is also where I found the image below.

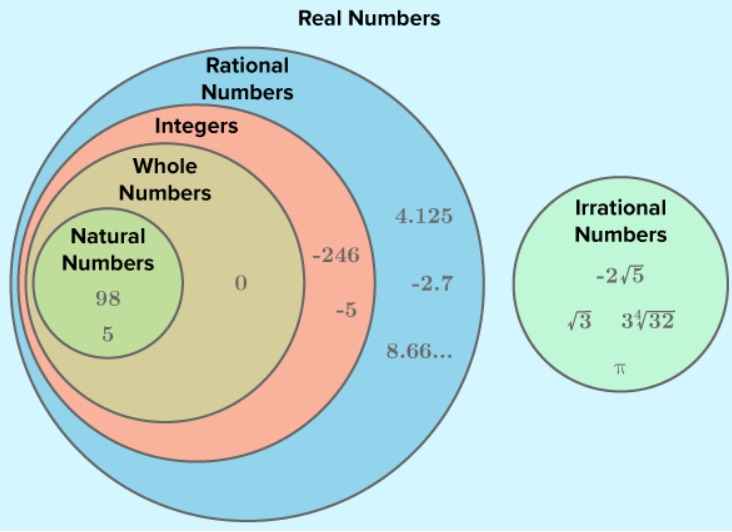
Natural numbers, also known as counting numbers, are the numbers we use when we use for counting objects: 1, 2, 3 and so on. They’re easy to understand because they represent tangible quantities. We count things all the time and we have context for them.

Whole numbers include the natural numbers and zero. This is where it gets tricky. We don’t usually say “Hey, no fair, I got 0 cookies.” Or “Look. Do you see how there’s zero birds in the sky?”

We technically can “see” zero though. If you have a pile of money sitting in front of you and I have nothing, I know that I can’t buy anything of value because I have nothing of value to trade. I have zero dollars.

Important things to know about zero

• It has a place on the number line.
• It can be used to represent the value of a digit.
• It has properties for every operation. We won’t talk about this today, but you can explore examples of the identity property of zero here.

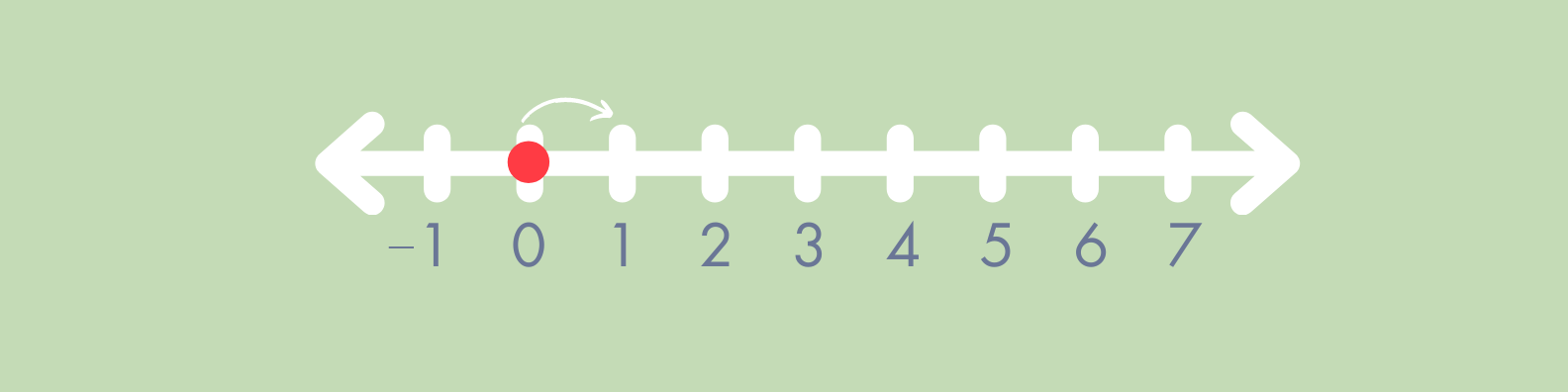
Zero and the number line

Zero holds an important spot on the number line. When kids struggle with fractions, it can be because they don’t understand the relationship between numbers on the number line. We start by teaching fractions with values less than 1, but unless we’ve explicitly talked about 0, that’s a hard concept to grasp. I talked a bit about this in “why number paths should be used instead of number lines”.

When students are used to talking about zero and seeing its value represented, they have the basis to understand that these fractions (the ones with values less than 1) are numbers that live between 0 and 1 on the number line. The closer those numbers are to 0, the lesser the value.

Zero and place value

Let’s consider the number 302. In this number, 0 is the numeral used to represent the value of the tens place. Sometimes, it’s mistakenly referred to as a placeholder. The term placeholder implies that it’s holding the spot for another digit. But 0 is a digit and it represents the value of its position in a number.

The misconception is sometimes generalized to the idea that zero means ‘nothingness’ in all contexts. 

If we use base ten blocks to represent 302, it looks like this:

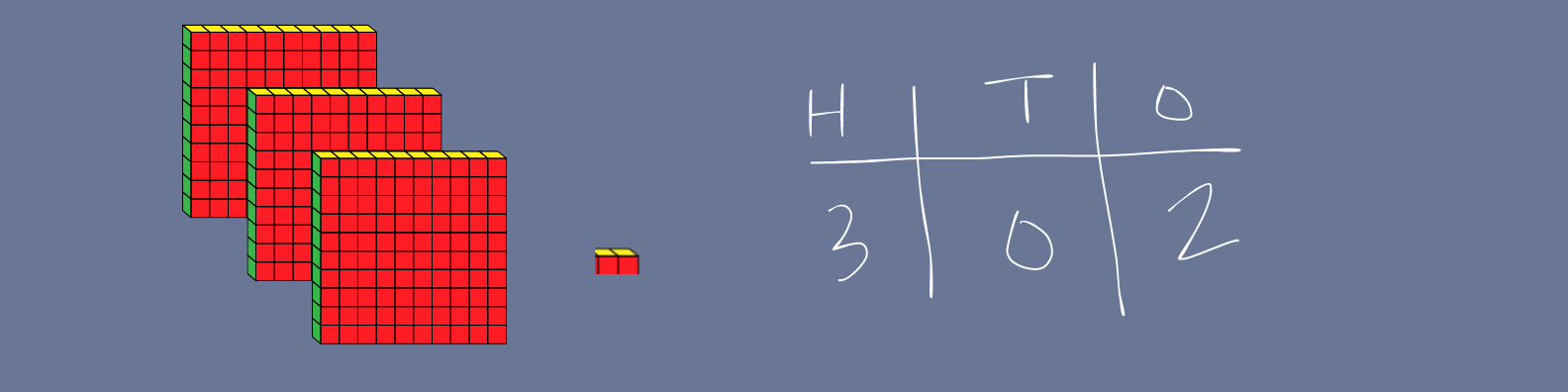
We can see the 3 has a value of three groups of one hundred, the 0 shows there are no groups of ten, and the 2 represents two ones. This becomes critical for later work with decimals.

When students understand the meaning of the value zero, they are less likely to struggle with ideas like grouping and ungrouping when it comes to subtraction.

While zero may literally mean nothing, it has huge implications when it comes to place value understanding. By teaching zero effectively, we can help our students build a strong mathematical foundation.