If you’ve ever taught odd and even numbers, you’ve probably heard the usual explanations.

• “Even numbers make a flat top.”
• “Odd numbers have a bump.”
• “Just look at the ones place.”

And maybe your students even seem to get it. They can sort numbers. They can check if a tower lines up. They can tell you that 17 ends in a 7, so it’s odd. But here’s the question: Do they know why?

Tricks can help kids name a number. But they don’t help them understand it.

What the Tricks Miss

Let’s take a closer look at some of the most common odd/even strategies:

• The “flat top” rule: This one usually comes with cubes. Kids build two towers to compare. If the tops are flat when they’re lined up next to each other, the number is even. While this technically works, we’re teaching kids a concept based on appearance not mathematics.
  
• Ones-place shortcut: This is the idea that if a number ends in 1, 3, 5, 7, or 9, it’s odd, which is technically true. The problem is students aren’t reasoning about two equal groups; they’re memorizing a pattern with no connection to the math.
  
• Digital sorting games: These often focus on speed: sort the numbers, tap the evens, get points. There’s no time for thinking, no models, and no language which means no conceptual understanding.

These approaches may seem harmless, but they send the wrong message: that math is about spotting something quickly, not making sense of it.

As Doug Clements reminds us, “Early math is cognitively fundamental. It’s not just about numbers and shapes. There’s reasoning and thinking embedded in what we do in early mathematics that forms a foundation for years to come.” If we want students to build that foundation, we can’t skip the thinking.

Start with the Structure

Even means a number can be split into two equal groups. Odd means it can’t, that there will be a remainder of one leftover when a group is divided into two parts.

We want students to see that. Not just label it.

That’s where the Compare structure comes in. Using this structure as a model, we decompose one set into two parts and line up the two sets, matching one cube to one cube to see if each train has the same amount, or if there’s one leftover. We ask: do the trains have the same amount?

If they have the same amount, that means the groups are equal and the original set we started with had an even value. If there’s one leftover, that means the value of the original set is odd.

💡In the traditional Compare structure, the leftover could be any value because you’re comparing two distinct quantities. When using this structure to teach odd and even, if it’s odd, the left over will always have a value of one because we’re using it for different comparison purposes.

For example, if you decompose the number 8, each tower will have 4 cubes. Because they show equality, the number 8 is even. If you decompose the number 9, one tower will have an “extra”. That means it’s odd. (see the example below)

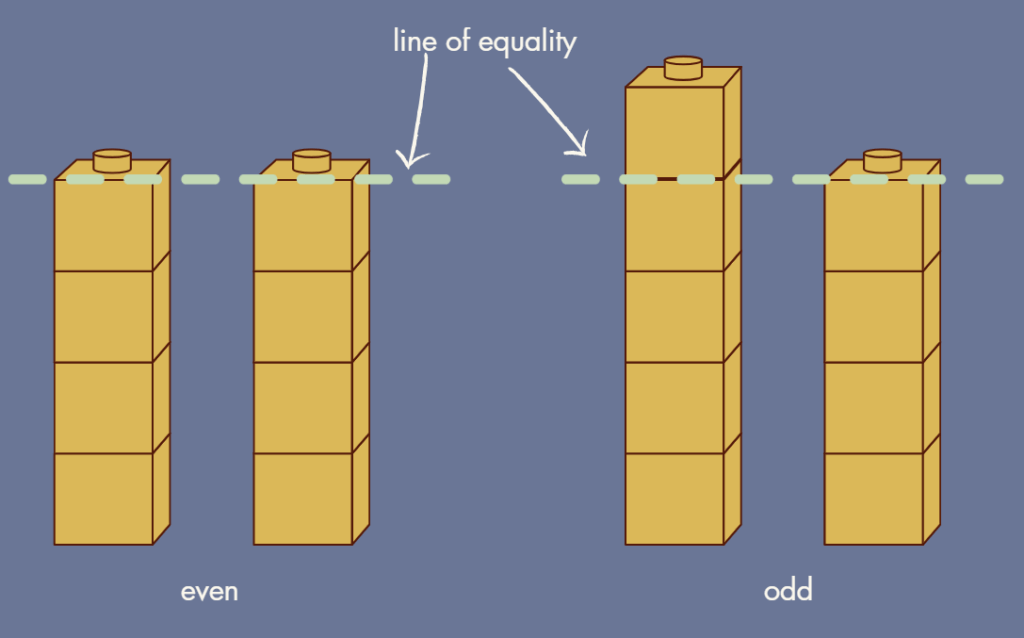
It’s simple, but more importantly, it’s meaningful. Students aren’t relying on what the number ends in. They’re reasoning about what it is: a quantity that can or can’t be shared equally.

Where the line of equality comes into play

In Structures of Equality, we use the term line of equality to describe the point up to which two values are equal. When students build with cubes and compare two towers, they can see exactly how far the match goes. That line shows equality.

Anything beyond the line of equality is what’s left over. It’s the extra. And when we’re teaching odd and even, that leftover is what shows us the number isn’t even. That’s how we know it’s odd. (see image above)

This idea builds directly on Doug Clements’ work with Match-Compare. In early math, children develop the idea of comparison by matching objects one-to-one and noticing what’s the same or different. We’re doing the same thing here, just with numbers and cube towers.

Why These Connections Matter

One of the most powerful things we can do for our students is help them connect ideas across math. Not just by chance, but on purpose.

If students have used the Compare structure before, then using it to explore odd and even isn’t something new. It’s something familiar. They’ve lined up cubes and matched sets before. Now they’re doing it again, with a new purpose.

And it works the other way, too. If odd and even is the first time they’re introduced to the Compare structure, they’re getting early experience with a model they’ll use later for comparing quantities in word problems. They’ll already understand what it means to have “one more” or “one less.” That understanding won’t feel like a brand new idea when it shows up again. It’ll feel connected.

We want our students to see math as a set of connected ideas, not isolated skills. That starts with us showing them how.

The Bottom Line

Odd and even isn’t a trivia game. It’s not about looking at the ones place or checking the shape of a tower. It’s about equality, matching, and whether two sets have the same value.

When we teach it with real models, real language, and real thinking, our students don’t just get the right answer. They understand why it’s right.