I’ve shared a lot about the 3 structures and how to implement them in your classroom. Today, we’re going to focus on one element that’s critical to all of the structures – equality.

A Brief Recap

If you’ve been following along, you know there are 3 essential elements to every structure. Here’s a quick refresher, just in case.

Structures of Equality (SoE) are graphic organizers that help students map out a math story. The 3 different SoEs are:

• Parts Equal Total
• Compare
• Repeated Equal Groups

A SoE is made of three crucial elements. They MUST:

• Contain values (numbers)
• Have labels (units of measure, the things you are counting…)
• Represent equality

When a student includes all three, it indicates comprehension.

These are the only models you need to diagram any problem type in the elementary Common Core standards.

Let’s talk about equality in math

You’re probably familiar with values and labels, but there’s a good chance you haven’t heard of the line of equality before. To understand what it is and why it’s important, we first need a common understanding of equality and what it means.

The root of equality is equal. I often hear this term interchanged with the phrase “the same as”. But this is a misrepresentation. Equal does not mean the same as. It means the same value as. It sounds like a small difference but that one word changes the entire meaning.

Here are a few examples: 

• 3 + 2 equals 5, but they are not the same. If I have 3 one-dollar bills and 2 one-dollar bills, that’s different from having a five-dollar bill.
• 4 equals 4, but they are not necessarily the same. If I have 4 ten-dollar bills that’s different from having 4 one-dollar bills. The amount of bills is the same but the value of those bills is not.

Understanding that equal means “the same value as” has huge implications in math. Valerie Faulkner, retired NC State Professor and education consultant, expands on this idea in her article* “Equality is not the ‘same as’”.

When equality is easy to see

When students understand where equality exists, they know how to use a diagram to accurately represent a situation. They understand what is happening within the problem and then can successfully write an equation to represent the diagram. 

Let’s take a look at a few examples where equality is easy to recognize:

In Parts Equal Total and Repeated Equal Groups models, the equality is evident by how the parts bars, when composed, line up with the total bar. This shows that the parts and the total are equal. This is important because it allows students to visualize how when the parts are composed, they have the same value as the total, or how the total can be decomposed into equal parts.

What about the line of equality?

In number stories that describe comparison situations, the equality is not so evident. And this is where the line of equality becomes crucial for comprehension.

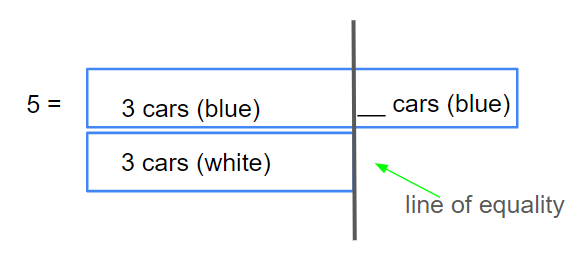
The line of equality is a line that shows where two linear sets are equal and separates the more, or extra. It is a key understanding students need to be successful when solving word problems. Regardless of the situation or operation, there is equality within every story.

In the Compare model, the line of equality shows the point up to which the sets have the same value. It makes it easy for students to visualize “the more” or “the fewer”, allowing them to understand the value of the unknown and then solve for it.

When students can identify the line of equality, it demonstrates their understanding of the problem. When students comprehend what the problem is asking and they apply previously taught strategies, they can solve any word problem that comes their way. 

As students progress through the grades, they are often asked to write or choose an equation that represents the story problem given. Students who can diagram those stories using a SoE have a much easier time managing this request.

Conclusion

The line of equality helps students conceptualize an abstract idea. This is especially evident in the Compare problems. The line of equality allows students to see the point up to which the models are equal.

In this example, we can see both sets of cars contain a set of 3. But the blue cars also have some more. We can understand that the difference will be 3 plus more to compose the total number of blue cars, or the total number of blue cars can be decomposed into 3 and the rest.

The use of SoE aids in flexibility with problem-solving, allowing students to make sense of what is happening in story problems.

Would you like to see more examples? Comment below or send me a word problem at julie@structureofequality.com, and I’ll show you how to solve it in a future blog or email.

*Faulkner, Valerie. “Equality Is Not the Same As…” Valerie Faulkner Math Club, https://valeriefaulknermathclub.com/2012/10/03/equality-is-not-the-same-as/, Published October 3, 2012. Accessed November 6, 2023.