November 29, 2023
If you’ve been following along, you know that I created Structures of Equality (SoE) as a reading comprehension tool to help students understand how to solve word problems. You’ve also heard me talk a lot about making sense in mathematics. Today, we’ll explore what it means to think like a mathematician. This post is about the explicit connections between SoE and the standards for mathematical practice.
If you’re new to SoE, I encourage you to familiarize yourself with them before jumping into the text below.
Let’s start with the Standards for Mathematical Practice
The research-based standards were developed to reform the way we’ve traditionally thought about mathematics. Math is not a series of steps or procedures, or rote memorization. It’s complex and dynamic and requires critical thinking skills. The practice standards help us understand how to think about math deeply instead of widely.
There are 8 practice standards that can help us guide best practices as we engage students in math.
- Make sense of problems and persevere in solving them.
- Reason abstractly and quantitatively.
- Construct viable arguments and critique the reasoning of others.
- Model with mathematics.
- Use appropriate tools strategically.
- Attend to precision.
- Look for and make use of structure.
- Look for and express regularity in repeated reasoning.
These distinct, but interrelated behaviors, can be grouped according to a few key ideas. The graphics from Miami-Dade County Public Schools and the San Francisco Unified School District help us visualize the connections between the standards.
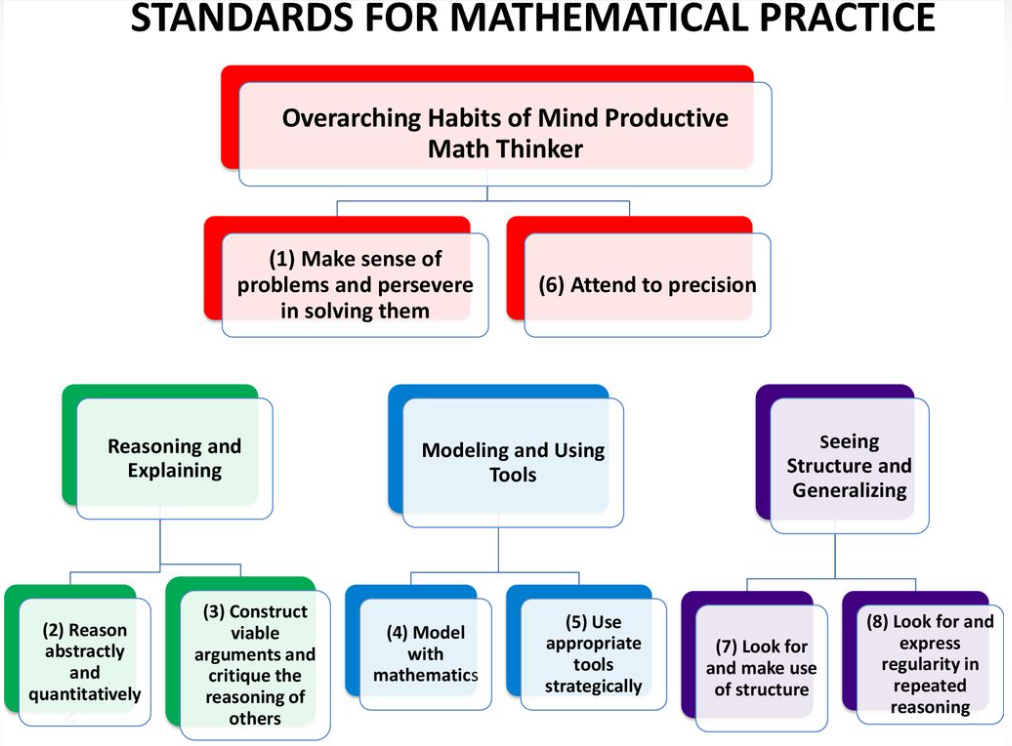
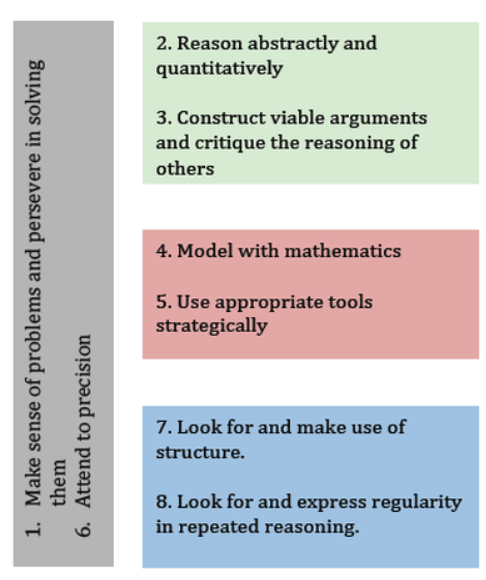
Critical thinking and problem-solving are emphasized over conventional approaches, which tend to be more about memorization and steps.
This is why it takes substantial time upfront and explicit teaching of the SoE for students to internalize them. We are asking them to engage in higher-order thinking which takes time to develop.
A look at the relationship between the practice standards and SoE
What sets SoE apart from other problem-solving approaches is that when a student uses the structures to model a number story, it is an indication of comprehension. It’s impossible to represent a situation with an SoE if there is not a complete understanding of what is happening in the problem.
The use of the structures requires deep exploration of word problems, and each one lends itself to all 8 of the practice standards. Wichita Public Schools created a guidance document that supports the implementation of the Standards for Mathematical Practice (SMP). We will use this to explore the relationship between SoE and SMPs.
I’ve listed below the tasks and actions from the SMP that students show every time they use SoE to diagram the situations in story problems.
Overarching Habits
Make sense of problems and persevere in solving them. Attend to precision. (SMP 1 & 6)
To demonstrate these standards, students:
- “analyze a problem”
- “see relationships”
- “label quantities appropriately”
Reasoning and Explaining
Reason abstractly and quantitatively. Construct viable arguments and critique the reasoning of others. (SMP 2 & 3)

To demonstrate these standards, students are asked to:
- “make sense of quantities and the relationships”
- “create a representation of the problem”
- “provide evidence”
Modeling and Using Tools:
Model with mathematics. Use appropriate tools strategically. (SMP 4 & 5)
To demonstrate these standards, students are asked to:
- “simplify complex problems and identify important quantities to look at relationships”
- “describe a situation with…a diagram”
- “ask themselves ‘How can I represent this mathematically?’”
- “use mathematical models to visualize and analyze information”
Seeing Structure and Generalizing
Look for and make use of structure. Look for and express regularity in repeated reasoning. (SMP 7 & 8)

To demonstrate these standards, students are asked to:
- “see complicated things as…being composed of several objects”
- “look for structure within the mathematics (i.e. decomposing numbers)”
- “see the overall process of the problem and still attend to the details”
What does this look like in practice?
SoE have 3 components, including the requirement for labeled representations. These labels help students understand the meaning of the numerals and their context within the number story. Each model is drawn to precisely show the relationship between the quantities. For example, the line of equality in a Compare structure demonstrates the point up to which two quantities are equal.
The line of equality provides evidence that the longer bar can be decomposed into a value of 3 and an unknown value.
In the Parts Equal Total and Repeated Equal Groups structures, the bars in the model are the same length and show that the total is equal to the value of the parts. Students use part sizes to represent numeral values.
In Repeated Equal Groups structures, the parts are drawn the same size to represent they all have the same value.
In Parts Equal Total structures, students analyze the size of the parts and draw them according to the value they represent when the total is decomposed. They can visually show the relationship between the parts and then use the model as justification for their solutions.
In the problem below, the unknown value is slightly greater than the known part. Students can refer to their diagrams to make sure the value they attained when solving makes sense.
Successfully representing story problems with SoE requires students to integrate various practice standards, as shown above.
Conclusion
In this exploration of Structures of Equality (SoE) and their connection to the Standards for Mathematical Practice (SMP), we’ve seen the essential role SoE play in developing mathematical proficiency. It’s not just a novel approach; it serves as the pathway to deep comprehension of word problems.
The key takeaways are clear: SoE require thoughtful and deliberate implementation, encouraging students to access and understand story problems at the highest level. Rather than relying on step-by-step procedures or tips and tricks, SoE promote critical thinking and problem-solving skills, aligning with the research-based SMPs.
As educators and parents, we can help students embrace the structures as tools to solve problems and understand the underlying mathematical principles.
The Core Standards. “Mathematics Practice.” The Core Standards, https://www.thecorestandards.org/Math/Practice/. Accessed 11 November 2023.
Achieve the Core. “Implementing Standards for Mathematical Practices (Updated 2016).” Peer and Pedagogy, https://achievethecore.org/peersandpedagogy/wp-content/uploads/2016/06/Implementing-Standards-for-Mathematical-Practices-Updated-2016.pdf. Accessed 11 November 2023
Common Core graphics from:
San Francisco Unified School District. “Standards for Mathematical Practice.” SFUSD Math, https://www.sfusdmath.org/standards-for-math-practice.html. Accessed 11 November 2023.
“Standards for Mathematical Practice.” SlidePlayer, https://slideplayer.com/slide/14502022/. Accessed 11 November 2023.