Walk into most kindergarten classrooms and you’ll hear a familiar question: “Is this equal?” It might be a teacher holding up two sets of crayons, or asking about groups of cookies or stacks of cubes. The goal is to spark comparison, to help students begin reasoning about quantity.

But too often, those early conversations focus only on counts of similar objects: comparing cookies to cookies or crayons to crayons. That’s where confusion starts.

We often hear the question: “How do I help my student understand the equal sign?”
But here’s the better question: “How do I help them understand equal?”

What Does “Equal” Really Mean?

It’s common to teach that equal means ‘the same as’. And while that might feel helpful at first, it’s not quite right.

Equal really means ‘the same value as’.

That’s a big difference.

I’ve been in classrooms with 6th graders who will argue that 8 = 5 + 3 is not true. They view the equal sign as a symbol only, and mistakenly think of it as a directional one at that. 

If I write 5 + 3 = 8, they’ll nod their heads vigorously. “Yes, that’s true.” But they’re convinced that 8 = 5 + 3 is incorrect.

The fix? Helping them understand the equal symbol as ‘the same value as’.

Then, you can ask what’s the value of 5 plus 3. They’ll respond 8 and you can then ask, does 8 equal 8; do they have the same value? 

But often we introduce equal to mean ‘the same as’ and it sets students up for misconceptions like these later down the road.

It Starts with Language, Not Symbols

The equal sign is abstract. If students haven’t built a concept of what “equal” means, then that symbol doesn’t hold meaning. It becomes something to memorize, not something to understand.

This is why we start with language.

We want students talking. About what it means to be equal or not equal, and how they know. That conversation lays the foundation for understanding.

Here’s how it might look and sound in a classroom:

You could direct 5 students to stand in one area, and 5 students to stand in another area. Then, have a conversation around equality.

Ask: Are these groups equal? Yes, this is a group of 5 students and this is a group of 5 students, even though the students in each group don’t look the same.

You can then take one of the groups and decompose into 3 students and 2 students, still standing in a contained area. Ask: What about now? Do we still have 5 students here? Do we still have 5 students over there (pointing to the other group)?

Then reinforce the idea that even though the groups aren’t exactly the same, they have the same value.

Non-examples help here too. You might call up a group of 4 students and another group of 6 students. Ask: Are they equal? No, they’re both groups of students, but the amount of students is different. They’re not equal. 4 does not have the same value as 6.

You can relate this to their prior knowledge and pose questions to relate equal to the idea of fair and not fair. Ask: What if I gave you 3 cookies and your classmate 5 cookies? Would that be fair? No, because those amounts are not equal. 

We’re not rushing to the symbol. We’re connecting it to ideas students already understand. By beginning with language and modeling ideas clearly, we help students attach meaning to symbols when they’re ready.

This approach aligns with the CRA Framework: Concrete, Representational, Abstract. It’s not a linear progression, but a continuum and students will shift between the phases. That might look like:

Concrete: Students using cubes or a balance scale to compare two amounts. For example, placing five cubes on each side of a balance and noticing it stays level, showing that the two sides are equal in value . Or placing different amounts of the same object and noticing the imbalance to explore not equal, or not having the same value.

Representational: Drawing what they built, like two sets of five cubes or an unbalanced scale with three on one side and five on the other, to show visually what equal and not equal look like.

Abstract: Writing equations to show those relationships. For equal, they might write 5 = 5. For not equal, they might eventually write 3 < 5 or 4 + 1 ≠ 6.

What matters is that students are making connections. Not just between numbers, but between the ways we can say and symbolically represent what’s happening. 

Beyond Kindergarten:

Imagine this: In a 3rd grade classroom, the teacher writes the following equation on the board. 3 + 4 = ___ + 1. Students are asked to solve.

As the teacher walks around, they notice most students filled the blank with 7. They saw an equal sign and viewed it as a direction. Add the numbers on the left and put the total after the equal sign.

They don’t understand that they are trying to make the equation balanced, to have the same value on both sides. If they understood that idea, they would notice that 3 + 4 equals 7, so __ + 1 would also need to equal 7. And clearly 1 + 7 can not be equal to 7. It doesn’t make sense.

Our work with the concept of equality lays the foundation for critical concepts like these that students will grapple with in later math, such as balancing equations in algebra.

How Structures of Equality (SoE) Models Help

In the Structure of Equality framework, we use visual models that help students see equality in action.

• In a Parts Equal Total model, the total bar is equal to the bar that is decomposed into parts. They have the same value.

If we go back to the example above: 3 + 4 = __ + 1, we can see how this model could help students visualize the concept of equality. They could draw one bar decomposed into 3 and 4, and then understanding the equal symbol, they would know to draw the bar below the same size and decompose it into an unknown and 6. They would recognize that both sides of the equation are equal and each have a value of 7.

To help create a more explicit connection between ‘naked’ equations like these and Structures of Equality, you could ask students to create number stories that match the structure. For example:

Sedrick had 3 red jelly beans and 4 yellow jelly beans. His sister had 1 red jelly bean. How many more jelly beans does his sister need to have an equal number of jelly beans as Sedrick?

This is a powerful extension to your work around the structures, and also a way to build connections across content areas.

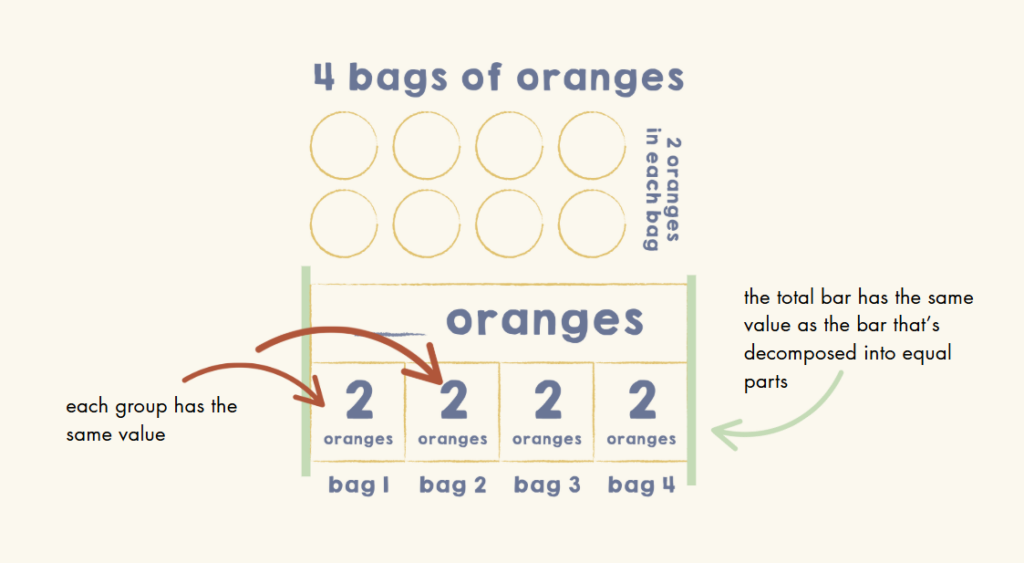
• In a Repeated Equal Groups model, not only does each group have the same value, but the total has the same value as the composed groups. They are equal.

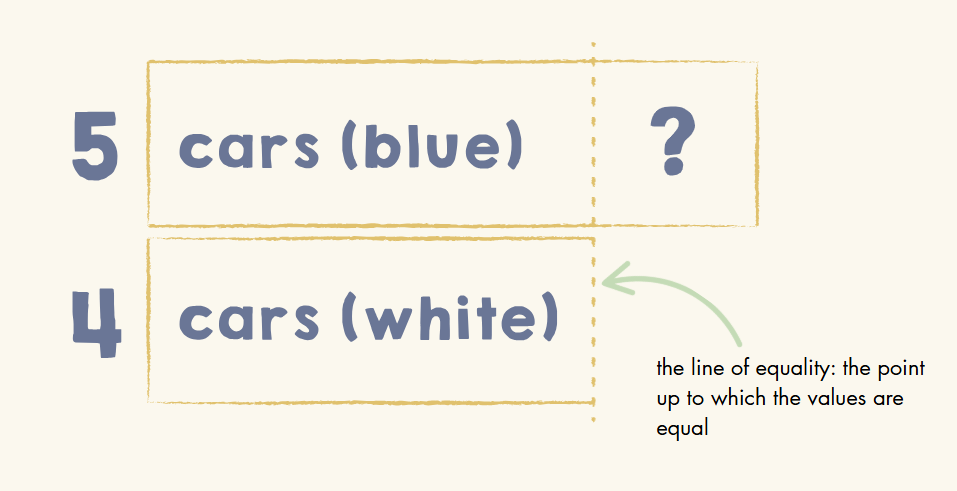
• Compare models use a line of equality to show that up to that point, the value of the longer bar is equal to the value of the shorter bar.

These representations help students work within the representational stage of the CRA framework, bridging the gap from real-world thinking to symbolic expression.

When the Symbols Come Too Soon

Sometimes, curriculum pacing guides or required lessons ask teachers to introduce the equal sign before students are truly ready. This is a real challenge. If the understanding isn’t there yet, the symbol won’t carry meaning.

In our post on teaching greater than and less than, we shared advice for this exact situation. If you’re required to use symbols early, don’t start with the symbol itself. Start with the conversation.

You might say,

• “This symbol means equal. It’s just a way to show what we already talked about.”
• “Remember when we said the two sides of the balance had the same value? We can show that with this symbol: =.”

By linking symbols to the language and relationships students already understand, you’re giving the abstract meaning a place to live.

For Teachers: What If…

How do I recognize when a student is ready to use the equal sign symbolically?
Look for students who can explain why two amounts are equal (or not equal) without relying on how they look. If they say things like, “They have the same total.” or “These two groups are equal in value even though they’re composed differently,” they’re likely ready to begin seeing the symbol as a representation of that relationship.

What if I’m required to introduce the symbol before my students are ready?
Use the symbol as a label for what they already know. Integrate it gently into the language you’re already using, and avoid focusing on equations alone. Continue reinforcing meaning through visuals and conversation.

How do I help students who already have misconceptions?
Start by naming the misconception aloud: “Some people think equal means the same. For example, $5 equals $5. That’s true. They have the same value. But if you have a $5 bill and I have 5 one-dollar bills, that’s not the same.”

For Caregivers: Frequently Asked Questions

If my child is learning about the equal sign in homework but doesn’t seem to understand it, how should I respond?
Talk through the problem together. Ask what each part of the equation means and how they know it’s true. Try building the quantities with blocks or other items to help them visualize it.

Are there simple activities we can do at home to explore ideas of equal and not equal?
Yes! Compare portions at snack time, line up toy trains of equal length but different parts, or use a kitchen scale to balance different objects. Then ask, “Are these equal? Why or why not?”

Why does it matter if we talk about value instead of just counting things?
Because equal can be reliant on unit, not just how many. Three coins and three paper clips are not equal in weight but they are equal in amount.. Talking about value helps your child understand deeper math ideas later.

A Final Thought

Helping students understand “equal” is not about telling them what the equal sign means. It’s about creating opportunities for them to build that understanding conversation by conversation.

Start with meaning and let the symbols come later. And when they do, our students will be ready.