December 18, 2024
Does bar size matter for accuracy in visual math representations?
Structures of Equality (SoE) are visual representations that model what is happening in a number story. Although they use bar models as their basis, they’re superior to the basic bar model because they cannot be drawn accurately without understanding the number story. They’re a reading comprehension tool that helps students visually represent the relationships between quantities.
When to hold students accountable
This brings up an important question, one I’m often asked by teachers.

The answer to this is both simple and complicated. The simple answer is this: hold students accountable when they’re ready. You’ll know they’re ready when they start to ask questions like, “Wait, shouldn’t the part of the bar that shows 9 be bigger than the part that shows 4?”
But getting them there is a bit more complicated.
As a teacher, you should always draw your structures to be accurate visual representations of the number stories you’re working with. The point of models is for students to tangibly see what’s happening so they can make sense of the mathematics.
Equality is a key component of the structures. When drawing both the Parts Equal Total (PET) and Repeated Equal Groups (REG) structures, both bars should be the same size. Encourage students to do this from the start. It’s the values within each bar that may not be as accurate initially.
When you draw your structures, thinking aloud is an effective way to model how you’re making connections between what’s happening in the number story and what you’re drawing. Let’s talk about what that could sound like.
Using think-alouds while modeling the structures
Parts Equal Total (PET)
We’ll start with a PET model. This is the model to use when a story describes 2 or more parts being put together (composed) or a total being decomposed into 2 or more parts.

💭 After discussing the context of the story with your students, a think-aloud might sound like this, “We know our total is 8 balloons so I’m going to draw that bar first. It’s decomposed into 3 and something else. I’ll draw that bar to be the same size and then split it so I can show the parts.”
This calls attention to both bars being equal and allows your students to focus mainly on showing their understanding of the math main idea. Until students have internalized the structures, we want to decrease their cognitive load – the amount of ideas they can work with at once.
When you’re ready to start your think-aloud related to the sizes of the parts, start with problems that have a larger discrepancy between the quantities. For example, use a problem such: Ms. Felder had 20 balloons. Three are read. The rest are yellow.
💭 Then your think-aloud will sound more like “I’ll decompose the bottom bar to show 3 balloons and an unknown amount. Since 3 is much smaller than 20, I’ll draw it smaller.” Students who are ready will start to do this on their own as well.
💭 You can also draw attention to the size of the bars as students are working independently. As you circulate to monitor, you might say something like “I noticed you drew this part of the bar much bigger than this part. Can you tell me about that?”
You can also pose similar questions when students are sharing their work with partners or the class. This way, all students are getting exposure to the concept. Eventually, they’ll begin to ask about the sizes of the parts of their bars and you can start to hold them accountable.
While PET focuses on part-whole relationships, REG highlights equal groups forming a total. Let’s look at how this structure works.
Repeated Equal Groups (REG)
The REG structure is used when equal parts are being composed to form a total or a total is decomposed into equal parts.

💭 In this case, the parts being equal is critical to understanding the math main idea. Your think-aloud should always include a statement like “I’m going to split this bar into equal groups to show they’re all the same size.”
Initially, you don’t need to hold your students accountable for doing the same. As the idea comes up in conversations with students and they’ve already drawn their models, you might pose questions like “I noticed (student name) drew all their parts exactly the same size. Why do you think they did that?” Once they can articulate an accurate response to this question, you can begin to encourage them to do the same.
Compare
Lastly, we have the Compare structure. In this case, the math main idea represents comparing two unique sets. A unique feature of the Compare structure is the line of equality, which shows where two linear sets are equal and separates the more, or extra. It makes it easy for students to visualize “the more” or “the fewer”, allowing them to understand the value of the unknown and then solve for it.
From the start, it’s important to hold students accountable for drawing their bars different sizes so they can draw the line of equality.
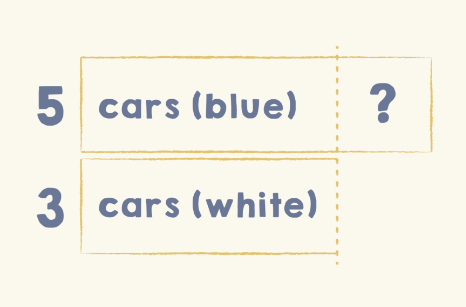
💭 This think-aloud will sound very similar to PET. “I know 5 cars is more than 3 cars so I’m going to make the bar that shows 5 longer. This is the point up to which they’re equal. Let me draw the line of equality here to decompose my 5 into 3 and some more.”
As students begin to have discussions about the size of the bars, start with values that have a much larger discrepancy such as 3 and 15. “I know 15 is a lot more than 3. Let me make this part (“the “more”) much longer.”
Conclusion
Remember, the ultimate goal is to make sure students understand the relationships between the quantities. Like other concepts in math, you can begin to get more nuanced as the problems grow more complex.
So, does bar size matter when it comes to modeling visual representations? Yes, but it’s a skill students learn over time. By modeling accurate structures, using think-alouds, and gradually building accountability, you create a foundation for students to make sense of math in a meaningful way.