The problem with traditional math education

I bet you’ve heard people say “I’m not good at math.” or “I’m not a math person.” Maybe you’ve even felt that way before. This idea comes up with students, their parents, and educators across content areas. Here’s what I found it usually means:

People who define themselves as not being good at math were often taught math as a series of steps to complete. They learned to memorize formulas and follow procedures. Or were never taught to comprehend, and likely didn’t use visual representation in math. They see math as abstract and irrelevant figures that are difficult to understand. Imagine how you’d feel about reading if all you learned how to do was decode words without understanding what they were saying.

The power of visual models in math

As students progress through school, math becomes more complex. Ideas are harder to conceptualize. But rather than taking the time to tackle them concretely or with visual representations, we teach with formulas and rote procedures. Students might think that drawing a picture is babyish, an unnecessary step.

But the truth is, visual representations are important at all levels of mathematics. They help students see the math. And when we can visualize what’s happening within a problem, it helps us understand abstract concepts. Students are able to communicate their understanding and interpretation of the problem. Consider this:

Greene, Kim. Understood. “Evidence-based math instruction: what you need to know” https://www.understood.org/articles/evidence-based-math-instruction-for-struggling-students

?Wow, that’s powerful.

What is an example of a visual representation in math?

Manipulatives, number lines, pictorial representations, diagrams, charts…these are all visual representations that can be used to show mathematical concepts. It’s an accurate depiction of a given problem’s mathematical quantities and relationships.
This is why I call Structures of Equality (SoE) a reading comprehension tool. Students visualize problems and draw a representation to show how they see the relationships within the number stories.

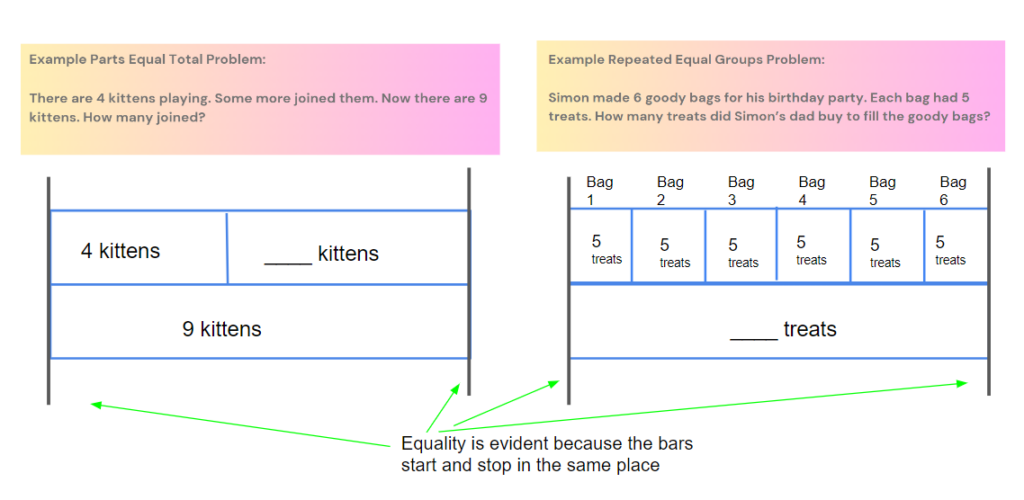
According to Dr. Valerie Faulkner, Ph.D, “Visual representations spark the visual part of the brain and help us to translate between fully embodied concrete objects and the numerical symbols we use to represent them. They provide the learner with stimulus that ‘fires’ the visual part of the brain. But beware –  not all visual representations are equally powerful! Representations that support the learner in processing numerical relationships in a structured and reliable way are critical to internalizing mathematical meanings and relationships. The Structures of Equality turn visual thinking into a linear and comparative tool that can then be used to interpret and develop mathematical ideas, relationships, and language from arithmetic to algebra to geometry.“

How exactly do visual representations help?

There’s been fascinating brain research conducted about what happens when students engage in tasks that use visual representations in math.

“When students work with symbols, such as numbers, they are using a different area of the brain than when they work with visual and spatial information, such as an array of dots… researchers found that mathematics learning and performance was optimized when the two areas of the brain were communicating (Park & Brannon, 2013). Additionally, they found that training students through visual representations improved students’ math performance significantly, even on numerical math, and that the visual training helped students more than numerical training.” 

Boaler, Jo. “Visual Math Improves Math Performance.” YouCubed, n.d., https://www.youcubed.org/resources/visual-math-improves-math-performance/

As we explore findings like these, it becomes evident why incorporating visual representations aligns seamlessly with the Common Core Standards for Mathematical Practice.

The Standards for Mathematical Practice

The Common Core Standards for Mathematical Practice were released in 2010, but are based on over 25 years of research about what makes students proficient at mathematics. There are 8 practices for students to develop in order to think critically about math, to understand it deeply. Practice Standard 4 is to model with mathematics. 

Why is it important to model with mathematics?

Mathematically proficient students can:

• identify important quantities in real-life situations
• model the relationship between quantities using tools such as diagrams and graphs
• analyze relationships and make conclusions

“They routinely interpret their mathematical results in the context of the situation and reflect on whether the results make sense, possibly improving the model if it has not served its purpose.” Common Core State Standards Initiative. “Standards for Mathematical Practice.” The Core Standards, https://www.thecorestandards.org/Math/Practice/

Conclusion

Using visual representations in math is a critical part of developing deep, conceptual understanding. Achievement is increased, impacting students’ mindsets. 

Imagine never again hearing 

• I’m not good at math. 
• This is boring. 
• Why do we have to learn this anyway?

Or having to watch another frustrated student give up and feel negatively about themselves. What if it was as simple as incorporating visual representations into your classroom?

Curious to know more about how you can support reading comprehension of word problems using visual models?