Did you know number lines shouldn’t be used until 2nd grade? I didn’t realize that for a long time. But as soon as I learned about number paths and how they help students conceptually, it made total sense. I changed my approach to make sure I was using the right tools at the right developmental stage.

What’s a number path and how is it different from a number line?

Let’s start with number lines. It turns out that finding an accurate working definition is harder than I thought. So I’ve come up with my own.

A number line is a visual representation of real numbers on a straight line that extends infinitely in both directions. In early math, this typically looks like a horizontal line with whole numbers placed at equal intervals.

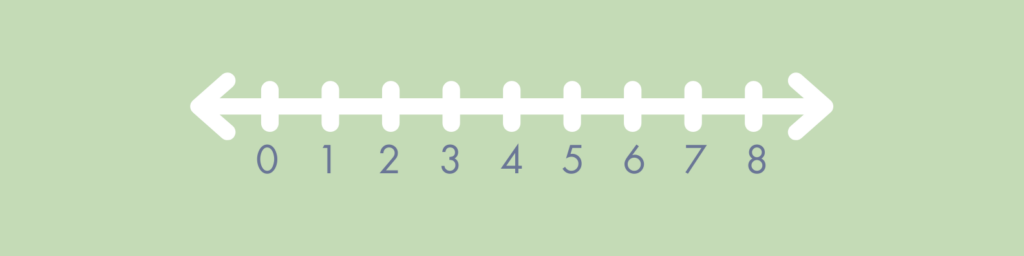
In contrast, a number path is a counting model where each square represents the value of the numeral inside.

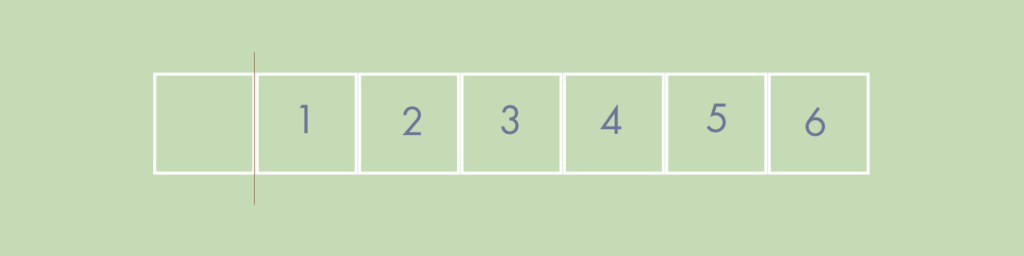
The distinction between a counting model and a length model (the number line) is important. “A number path helps our kids to see the objects in a line and be able to count individual objects instead of having to count a length.” (Build Math Minds)

Why are number lines problematic?

“When students start using a number line before they are ready, they are seeing spaces and lines rather than concrete quantities. In this sense, number lines take the actual quantity of a number out of student understanding.” (O’Neill, 2018)

Remember how I said it made total sense when I learned why I should use number paths instead of number lines? It’s because of this idea about quantity. The number line is an abstract tool we’re asking kids to use in a representational way.

The value of 1 encompasses the entire space between 0 and 1. It’s not a tick mark on a line. You might notice this confusion when a student starts counting on 0. Or when they end up a number above or below the value where they should land. (It’s also why fractions can be confusing. Now, that space suddenly has a value.)

Think of board games you’ve played before. You don’t put your game piece on the line in between spaces. You use it to fill the space. This is what a number path helps students see.
Once your students understand the value of each number conceptually, they can transition to a number line. This is a perfect example of what a Concrete Representational Abstract framework could look like in early math.

How to use a number path

Cristina Tondevold’s favorite uses for number paths are to build understanding around the value of a number and for addition and subtraction. 

She relates it to the idea I mentioned about understanding that a number is represented by the entire space. Let’s consider the representation of 4 on the number line vs the number path.

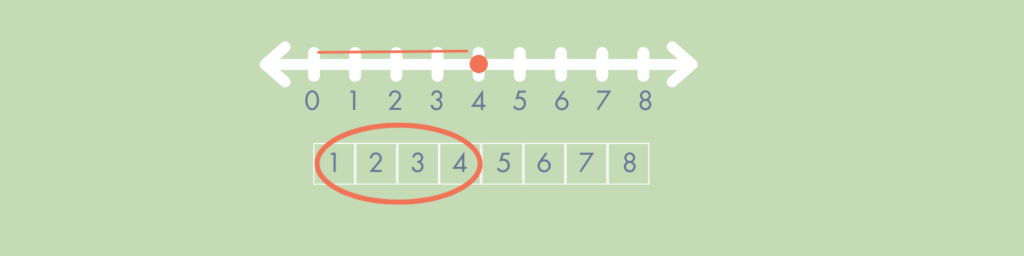
The number path model helps students see what 4 really means. Tondevold notes “This also leads into doing comparison-type problems where kids will show an amount and then show the other amount and talk about which one is more, which one is less.”

Which brings us to Structures of Equality (SoE).

How number paths support SoE

The reason the structures are so powerful is because they are visual representations of the situation as it’s occurring in the number story. Let’s take a look at this example from the NC DPI unpacking document.

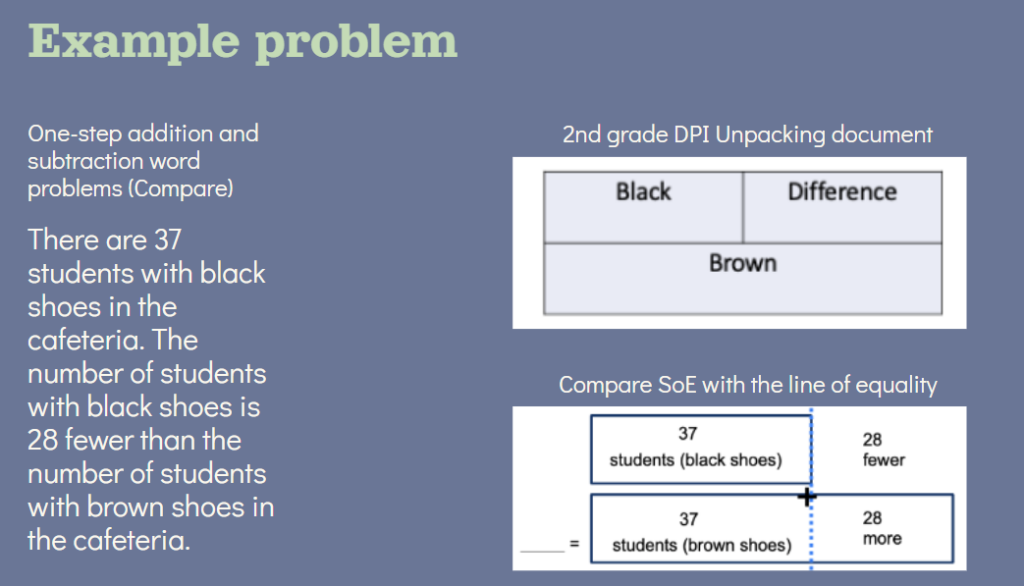
In the Compare SoE model, you can visually see the difference between the quantities of students with black shoes and students with brown shoes. Students who have experience working with number paths will be able to make this connection and understand the concept of ‘28 more’ in a tangible way.

The DPI model is problematic because it’s visually confusing. It looks like the total number of brown shoes has the same value as the black shoes and the difference between the two. The equation that would match this representation is black + difference = brown or the reciprocal. It does align with what is actually happening in the number story.

Conclusion

Introducing the number path before the number line makes a significant difference in how students develop their understanding of numbers and their values. Number paths allow your students to access quantities at the representational level and set them up for success with abstract concepts. As your students demonstrate conceptual understanding of numbers and their values (around mid-first grade), you can begin to transition them into the use of number lines.

For a few fun ideas on how to incorporate number path activities into early math education, check out this article from the Erikson Institute.