Conceptual vs procedural understanding: which is better? This is a conversation that comes up often among teachers. And people generally feel strongly one way or the other. Today we’ll define these terms, look at examples of each, and I’ll share my thoughts on this hot topic.

Defining conceptual and procedural knowledge

The root of procedural understanding is the word procedure, which is commonly defined as a process or a series of steps. It refers to what students are doing and is often associated with calculations. When we act procedurally, we are drawing upon our knowledge of formulas and algorithms.

At the root of conceptual understanding is the word concept, which is commonly defined as an idea. In math, it refers to the understanding students have around why the math they are doing works, and why it makes sense. Jean Soyke does an excellent job explaining conceptual understanding in math with a cooking analogy.

Conceptual vs procedural understanding: which is better?

They are often seen as opposite ends of the continuum and some have firmly planted themselves in either the conceptual or the procedural camp. I believe there’s a place for each. Instead of either/or, we need both.

Let’s look at a few examples. As we do, you’ll notice parallels in ideas around the phases of the Concrete Representational Abstract (CRA) approach.

Examples

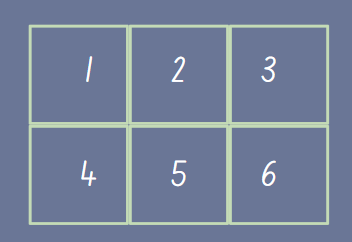
Let’s consider area. When students first learn about area, tiles are used to create arrays that represent the length and width of a rectangle. A 2 x 3 array would be represented as pictured below. Students are learning the concept that 2 x 3 means 2 groups of 3. They will count the 6 tiles to understand the total is 6. But that’s not all…

The idea of unit is critical here. If you’ve ever taught area or perimeter to students, you know they often confuse the labels for their solutions. The area of this rectangle is 6 square units, or 6 units squared.

Students can visually see the squares that compose the shape, helping them understand why their total will be in square units.

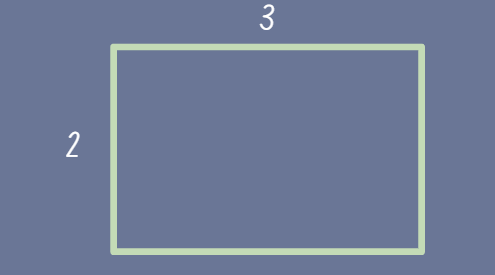
When we approach this same task procedurally, we use the formula area = length x width. Students would likely write the equation 3 x 2 = 6 or 2 x 3 = 6. It’s possible they have an accurate answer and could label it as square units without understanding why.

Once students have developed their conceptual understanding, it’s no longer necessary to lay out tiles or draw arrays. They will be able to connect the formula to a visual model. At this point, approaching the problem procedurally is the most efficient method.

Laying a conceptual foundation is critical for our students to become proficient mathematicians. As students progress through mathematics, they will have the knowledge needed to make connections across ideas, such as how area is related to volume.

An exception to my rule

While I believe there is a place for both conceptual and procedural thinking in math classrooms, I do have one exception – number stories. 

When students struggle with solving word problems, it’s almost always because they don’t understand what the problem is asking. Reading comprehension is at the heart of this issue. Procedural approaches like CUBES are problematic because they use a series of steps to work through conceptual ideas.

Conclusion

I think we’re having the wrong debate. It’s not about procedural vs conceptual and choosing one over the other. We should consider when each approach makes the most sense and use them accordingly.

Conceptual understanding is what allows students to grapple with complex ideas and make connections across different mathematical ideas. Procedural knowledge helps students with efficiency and accuracy. The key is to strike a balance that best supports students in their mathematical understanding.