Today, we’re going to talk about the idea of teaching fewer in math. We won’t explore the nuances between fewer and less (at least not today). But it will be helpful if we have a common definition:

▶ ️Fewer refers to the thing you are counting. It means it has a smaller or lesser value in comparison to something else. 

The idea of fewer is a difficult concept to understand. There are lots of reasons why, like you can’t actually see fewer. You can see a discrepancy between two amounts but fewer means you’re referring to a part that’s not there. No wonder why it challenges your students when they come across the idea in number stories!

Let’s start with a few real-life examples

Understanding the concept of fewer is not just about numbers; it’s about recognizing differences in everyday situations. Here are some simple, relatable examples that students can easily understand:

• Snack Time: Children might compare the number of cookies or crackers on their plate with their friends. They can identify which plate has fewer snacks and understand they have less to eat compared to others.

• Sharing: When playing with toys (or using materials such as crayons), children may notice that one friend has fewer blocks or dolls than another. They can learn to share and take turns, understanding that having fewer toys doesn’t mean they have less fun.

• Lineup Order: In lineups, such as during recess or when lining up to go back to the classroom, children might notice which line has fewer students waiting. They can learn about fairness and patience while waiting their turn.

We tend to use the word more when making comparisons because it feels more tangible. We can see and count more. By incorporating these relatable examples into classroom activities and discussions, you can begin to incorporate this language and help your students grasp the concept of fewer in a meaningful way.

Teaching fewer in math: how to do it.

It’s important to explicitly expose your students to the word fewer and what it means. This can and should be done in discussion around the context of story problems. If you’ve been around Structures of Equality (SoE) for a while, you know I am not referring to the idea of teaching it as a keyword. Your students need to understand what it means in the situation that is occurring in the story and how it plays out in the relationships between the values in the story.

I’d love for you to watch the video below to understand what I mean. It’s a quick walkthrough of how you can use the Compare structure to introduce and model a problem with fewer. As you watch, pay attention to:

• How we define the main math idea of the number story
• The use of sentence strips to visually represent the values
• How the line of equality helps students ‘see’ the more 
• The way more helps us understand the idea of fewer
• The strategy used to solve for the unknown values

? Compare Structure of Equality with fewer ?

Now that you have a better understanding of what this might look like with your students, let’s dig a little deeper.

Let’s break down teaching fewer in math in the context of a number story

The number story we modeled with the Compare structure is below. (If you didn’t watch it, it’s only 4 minutes long and this will make more sense if you do.)

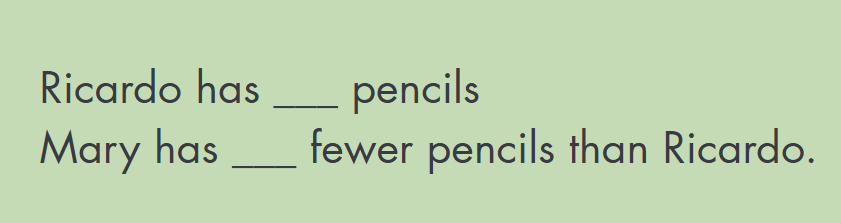
In the video, did you notice I never actually did any computations but was still able to figure out all the possible values we could ask students to solve for? Because we focused on the relationships, this problem became about sense-making, not about answer-getting. 

It’s an excellent example of one of the ways key words can be problematic. If I focused on the idea that fewer means less and told students they needed to subtract, they would come up with an accurate answer. But they would have no idea what the value represented! When we have comparison situations, we are finding the difference between two values, not removing a part.

We used the value of 10 for Ricardo’s pencils and said Mary had 2 fewer pencils. If we had gone straight to write a number sentence, we would come up with the equation 10 – 2 = 8. If you asked students to explain how this equation represents the above scenario, how many do you think would be successful without visually representing it with the Compare structure first? My guess is – not many.

Conclusion

Understanding and teaching the idea of fewer in math is fundamental but challenging. By exploring real-life examples, you can make this abstract concept more tangible and relatable. You can then shift into teaching this concept in the context of story problems. Using the Compare structure allows your students to focus on visual representations and relationships rather than computations. And fewer students confused about story problems is definitely a win!

Want to learn a bit more about how to use this structure? I have more videos posted on my YouTube channel. While you’re there, don’t forget to subscribe!