March 13, 2024
Arithmetic vs. mathematics: It’s more than just semantics.
I often hear these terms used interchangeably, but they are not the same. There is a significant difference between arithmetic and mathematics. When you hear the word math, what comes to mind? If you’re like most, you think of equations, operations, and formulas:
- 3 + 2 = 5
- 64 = 8
- a2 + b2 = c2
But math is far more than memorization and procedures. So what is mathematics?
According to the Oxford Languages dictionary, it’s defined as:
the abstract science of number, quantity, and space. Mathematics may be studied in its own right (pure mathematics), or as it is applied to other disciplines such as physics and engineering (applied mathematics).
(I don’t even know exactly what that means. But I know it’s a lot more than the basic problems I listed above.)
I love this article from The New Yorker that discusses how even mathematicians have trouble putting the definition of math into words. That’s because it’s so complex and nuanced. We may not all agree on how to define mathematics, but the research is clear about what it takes to be a proficient mathematician (more on that later).
Okay, then what about arithmetic? How is it different?
Arithmetic is the manipulation of numbers and is centered around the operations we use for computation. (Hmm, that sounds more like what we were talking about originally.)
So arithmetic and mathematics are not one and the same. Based on these definitions, arithmetic is only a piece of the mathematics puzzle (kind of like phonics is one part of learning to be a reader).
Tomayto, tomahto… does the difference between arithmetic and mathematics really matter?
If you’re asking me, it’s a resounding yes! Here’s why. In the United States in particular, we’ve come to think of mathematics in terms of arithmetic. Kids we consider “good mathematicians” are really just quick at calculations or memorization. They have the skills to perform rote and procedural tasks but don’t actually understand the mathematics.
This is one of the reasons we continually fall behind other countries when it comes to mathematical proficiency.
When we view mathematics through the lens of arithmetic, we align our teaching practices to this definition. The way we’ve traditionally approached our instruction includes:
- Tips and tricks (especially for word problems)
- Rote memorization
- “Drill and kill” skills-based activities
- Formulas, ‘rules’, and procedures
And the outcome is students who know how to perform operations without knowing how or why they work. To avoid this, we need to shift the way we think about math and redefine what it means to be “good at math.”
What it takes to become a proficient mathematician
The research behind the Science of Math concludes that math proficiency is a blend of:
- Concepts
- Procedures (arithmetic)
- Strategies (arithmetic)
- Reasoning
- Disposition
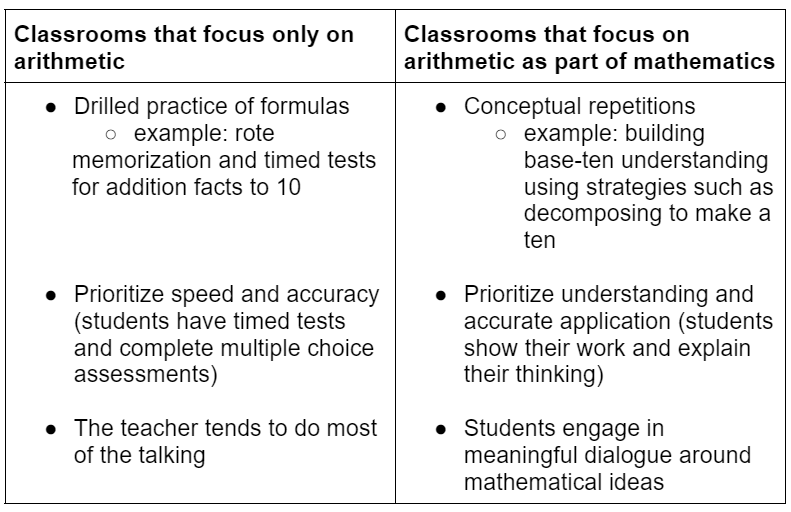
Classrooms with a focus on mathematics look and sound very different than those only focused on the arithmetic part of math.
Instruction in a classroom that focuses on math, not just arithmetic
Classrooms that build mathematically proficient students are the ones that go beyond the content. They engage students in meaningful tasks and develop the behaviors students use to approach those tasks. Math is about more than coming up with a solution; it includes how the solution is derived.
Here are a few indicators to help you see the difference:
The evolution of mathematics
Like most fields, mathematics has evolved over time. And it will continue to do so. Especially with advances in technology, like artificial intelligence. To ensure our students adapt to the times, we need to align our teaching practices to promote:
- Conceptual understanding
- Application of concepts
- Problem-solving and analysis
Ancient civilizations developed basic arithmetic for practical purposes like taxation and commerce. And even before that, tallies were kept on prehistoric bones for the purpose of counting. Then, in what seemed like an unimaginable feat, mathematicians helped send people to the moon. What if those on the ground at NASA only knew how to do rote procedures? Or guessed at what operation to use to adjust trajectories?
It’s our job to prepare our students to be proficient mathematicians. If we teach beyond arithmetic, we can ensure every child who leaves our classrooms is ready to tackle any innovations the future has in store.
Conclusion
The distinction between mathematics and arithmetic is more than semantics; it has significant implications for our classrooms and beyond. Arithmetic focuses on numerical manipulations but mathematics encompasses abstract concepts, reasoning, and problem-solving. Shifting our instructional approaches, and the way we think about mathematics in general, will better prepare our students for the challenges ahead.