November 29, 2023
Updated 12.17.2025
Structures of Equality (SoE) didn’t start out as a “math strategy.” It grew out of a need, a way to help students make sense of word problems by treating them like stories, not just problems to solve.
This post is about what happens when we slow down and focus on comprehension. We’ll look at how SoE lines up with the Standards for Mathematical Practice (SMPs) and why that matters for our teaching
Let’s talk about the Standards for Mathematical Practice
The SMPs were designed to shift how we think about math. Instead of steps and procedures, they focus on reasoning, communication, and sense-making. In other words, how students think mathematically, not just what they do.
There are 8 practice standards:
- Make sense of problems and persevere in solving them.
- Reason abstractly and quantitatively.
- Construct viable arguments and critique the reasoning of others.
- Model with mathematics.
- Use appropriate tools strategically.
- Attend to precision.
- Look for and make use of structure.
- Look for and express regularity in repeated reasoning.
They’re not meant to be taught in isolation. They work together, and good math instruction weaves them in naturally.. The graphics from Miami-Dade County Public Schools and the San Francisco Unified School District help us understand how they’re interrelated.
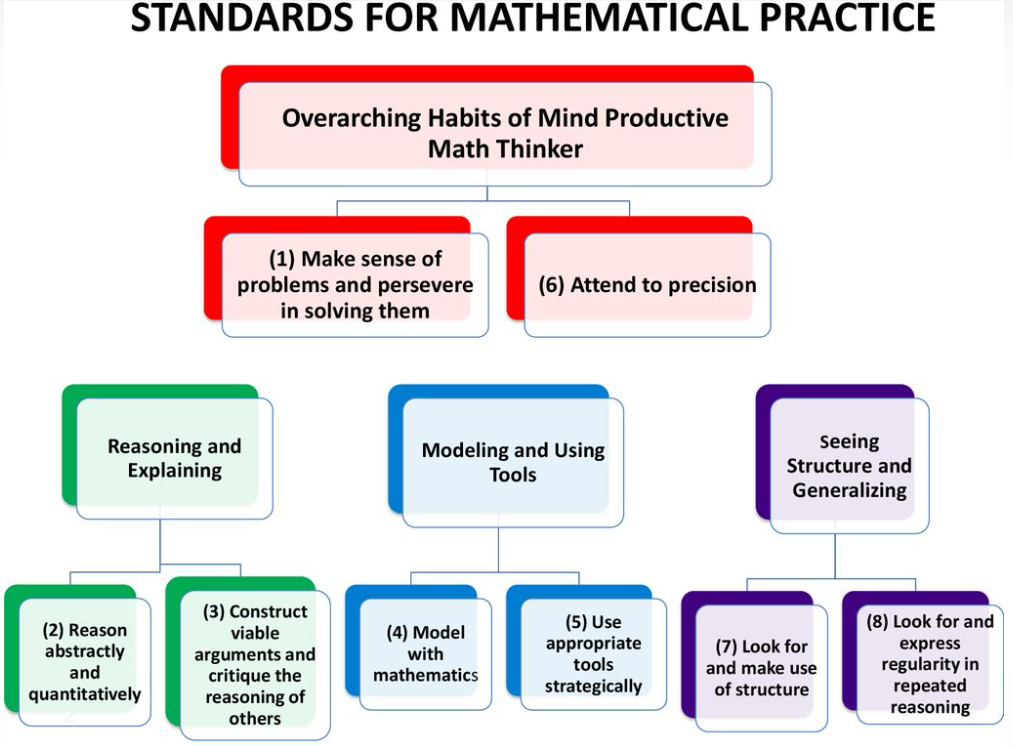

Why this connects to SoE
When students use a Structure of Equality to model a word problem, they’re showing you something big: they understand what’s happening in the story.
You can’t use SoE to draw a model unless you comprehend the situation. That’s what sets this approach apart. It’s about showing thinking. Every time a student builds a model using SoE, they’re making visible the exact kind of reasoning the SMPs are asking for.
Let’s break that down.
SMP 1 & 6: Make sense of problems and persevere in solving them. Attend to precision.
When students use SoE, they’re:
- Analyzing the story
- Labeling quantities carefully
- Thinking about what each number means in context
Those labels are doing the work of comprehension.

(SMP 2 & 3): Reason abstractly and quantitatively. Construct viable arguments and critique the reasoning of others.
With SoE, students are:
- Identifying relationships between quantities
- Representing the story in a model
- Using that model to justify their reasoning
The model becomes their explanation. You can point to it, talk about it, revise it. It becomes an integral part of the math conversation.

SMP 4 & 5: Model with mathematics. Use appropriate tools strategically.
When kids use SoE:
- They ask themselves, “How can I show what’s happening here?”
- They make decisions about which structure fits the story
- They visualize the situation before solving
Instead of randomly plugging numbers into an equation, students can actually see the relationships in the story.

SMP 7 & 8:Look for and make use of structure. Look for and express regularity in repeated reasoning.
SoE helps students:
- Recognize patterns across different problems
- Decompose and compose quantities
- Understand that even complex problems are built from familiar relationships
That’s why we spend time upfront helping students understand the math main ideas that are represented by three core structures: Compare, Parts Equal Total, and Repeated Equal Groups. Once they internalize these main ideas and structures, they start to notice them in all kinds of problems.

What this looks like in real classrooms
SoE have 3 components, including the requirement for labels. These labels help students understand the meaning of the numerals and their context within the number story. Each model is drawn to precisely show how the quantities relate.
In a Compare structure, the line of equality shows the point up to which two quantities are equal so students can easily see what’s leftover.

The line of equality proves that the longer bar can be decomposed into a value of 3 and an unknown value.
In Repeated Equal Groups, the columns are equal in length to show groups of the same size and the total being equal to the value of those composed groups.
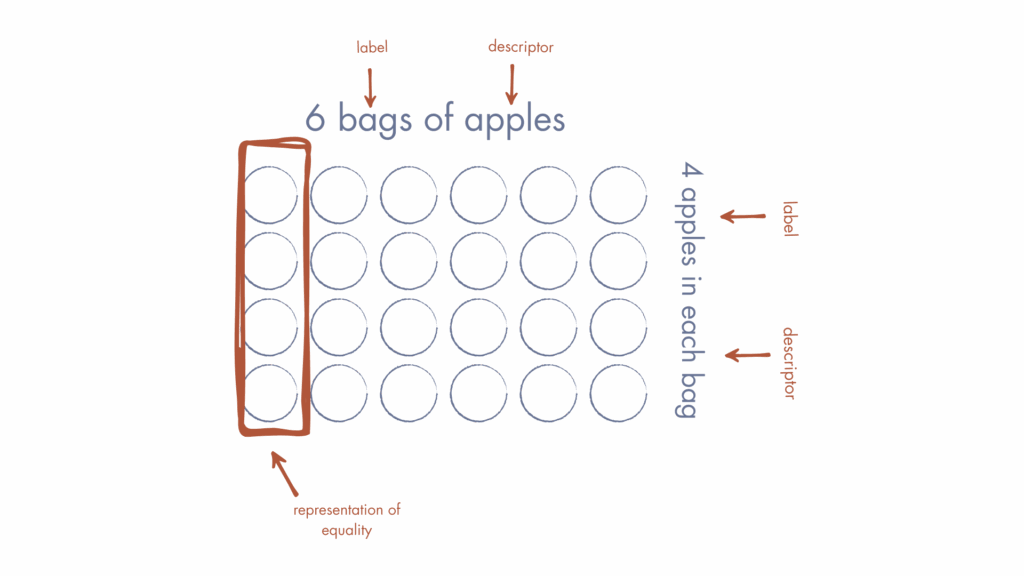
In Parts Equal Total, students show how different parts are composed, or come together to make a total, or how a total can be decomposed.

Each of these models is rooted in the idea of relationship. They help students see the math before they solve.
Conclusion
When students build a Structure of Equality, they’re doing way more than solving a word problem. They’re:
- Making sense of the story
- Choosing the right model based on relationships
- Justifying their thinking with precision
- Engaging with all eight Standards for Mathematical Practice
SoE isn’t a shortcut. It’s a framework that helps every student access rich, grade-level problems whether or not they’re confident in computation yet.
And for us as teachers, it gives us a window into their thinking. It helps us plan better questions, guide discussions, and support understanding where it’s needed most.
The Core Standards. “Mathematics Practice.” The Core Standards, https://www.thecorestandards.org/Math/Practice/. Accessed 11 November 2023.
Achieve the Core. “Implementing Standards for Mathematical Practices (Updated 2016).” Peer and Pedagogy, https://achievethecore.org/peersandpedagogy/wp-content/uploads/2016/06/Implementing-Standards-for-Mathematical-Practices-Updated-2016.pdf. Accessed 11 November 2023
Common Core graphics from:
San Francisco Unified School District. “Standards for Mathematical Practice.” SFUSD Math, https://www.sfusdmath.org/standards-for-math-practice.html. Accessed 11 November 2023.
“Standards for Mathematical Practice.” SlidePlayer, https://slideplayer.com/slide/14502022/. Accessed 11 November 2023.