October 12, 2023
“Make sense of problems and persevere in solving them” is the first of the 8 Standards for Mathematical Practice. Comprehension of word problems is also one of the most baffling tasks for teachers and students.
A Quick Refresher
In the last couple weeks, we explored two structures: Parts Equal Total and Repeated Equal Groups.

Parts Equal Total is used when a math story describes composing 2 or more parts to form a total, or when a math story describes decomposing a total into 2 or more parts. This blog post gives example problems and tips to put this structure into practice.

Repeated Equal Groups is a structure that’s helpful if a math story describes putting equal groups together (compose) or taking equal groups apart (decompose). To get a sense of what it looks like in action, you’ll find a helpful anecdote and more in last week’s blog.
When PET and REG overlap
Although these structures are for two distinct problem types, sometimes a problem has both equal groups & 2 or more parts and a total. When this happens, these stories can be represented using either structure.
These types of word problems are special because they allow students to be flexible in their thinking. They can also encourage dialogue about similarities and differences in the representations.
Here’s an example of a REG problem that also lends itself to a PET structure.
A bridge between additive and multiplicative thinking
When students first learn about multiplication with whole numbers, they are introduced to the idea of repeated addition. They learn strategies such as drawing circles to represent equal groups and using number lines. But these strategies are only effective if students understand what the word problems are asking in the first place.
When students don’t have a reading comprehension tool to understand what’s happening in a story problem, they tend to pull out the numbers and choose a random operation, or whatever operation they are learning about at the time.
As students move into multiplicative thinking, it’s essential they have comprehension so they can choose the correct operation to successfully solve word problems.
In 3rd grade, here’s an example from NC DPI’s Unpacking Document that shows how some students might demonstrate understanding of problems involving equal groups.
If a student doesn’t understand that this problem could be represented with a REG SoE, they might instead pull out the numbers and add them. They’ll likely know they’re looking for a total but may not have a way to organize their thinking.
When students are intimately familiar with SoE, they recognize there are 3 parts to this problem, each part is equal, and they are looking for a total. They can then use whatever strategies they want to solve the word problem.
If the solution is incorrect, their structure will help you identify the misconception in their thinking. Here’s how the above problem would look when correctly represented with PET and REG:
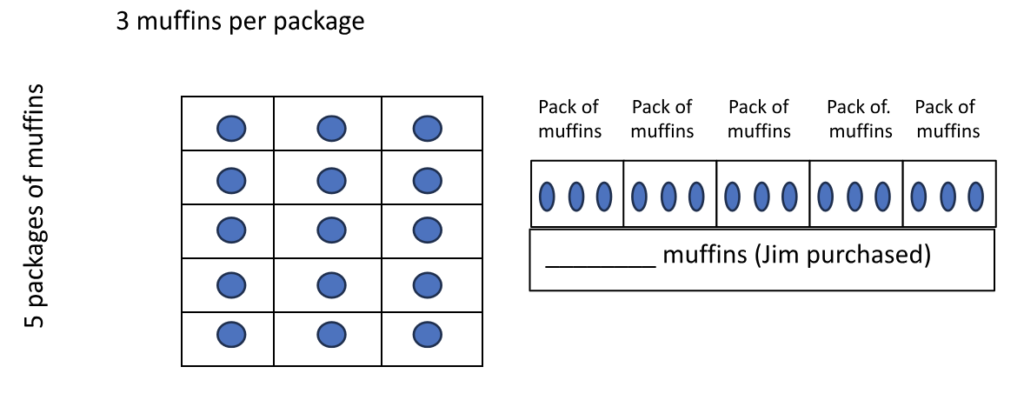
Conclusion
Parts Equal Total and Repeated Equal Groups provide a framework to help students process story problems and make sense of what is happening. There are some problem types that could be represented by either structure. By allowing students to use a reading comprehension tool to solve word problems, we begin to help them understand the “why” behind the “what”.
Next week, we’ll explore our final structure, Compare. Come back to check out that post. And if you want access to exclusive freebies, make sure you’re on my mailing list!