October 4, 2023
I once heard a math teacher describe word problems as “the bane of her existence”. I completely understand that sentiment. Students don’t know what the problem is asking, choose random operations, or give up completely. That’s why I created Structures of Equality.
If you haven’t been following along, you’ll probably want to start with my first blog post.
A Parts Equal Total Refresher
In last week’s blog, you got a deeper understanding of one of the Structures of Equality (SoE) called Parts Equal Total.
A student can use a Parts Equal Total SoE when a math story describes composing 2 or more parts to form a total or when a math story describes decomposing a total into 2 or more parts. It helps students understand the relationship between the parts and the total.
If you missed it, I encourage you to go back and check out the example problems and videos before we dive into the next structure.
Repeated Equal Groups
The next SoE we are going to explore is Repeated Equal Groups. This SoE is helpful if a math story describes putting equal groups together (compose) or taking a total and separating in into equal groups (decompose). As with all SoE, they have 3 distinct characteristics:
- Contain values (numbers)
- Have labels (units of measure, the things you are counting…)
- Represent equality
Although similar to bar models, these characteristics are what set SoE apart and help students understand the relationships within the math stories.
What does it look like in the classroom?
As I’ve mentioned in previous posts, SoE require systematic, explicit instruction. They’re challenging at first. But when students internalize them, they brim with confidence. I invite you into my classroom as we solve a Repeated Equal Groups multiplicative comparison problem.
I was visiting a 5th grade classroom and posed the above math story problem to them. The responses were less than enthusiastic. From their expressions and their body language, it was evident they didn’t believe they were capable of solving this problem. But I knew better!
So I started by asking them a few questions:
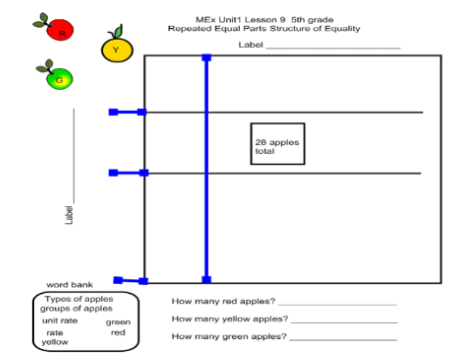
- What do you know about the apples? (We have 28. There are different kinds.)
- What do you know about the relationship between the apples? (4 times as many green as red & 2 times as many yellow as red)
- What are both the green and yellow apples being compared to? (red apples)
Light bulbs began to go off when I asked them the next question:
- If I had one red apple, how many yellow/green apples would I have?
We drew the apples on the chart (first column) and discussed that this was our unit rate. Each time we drew another apple unit (1 red, 2 yellow, 4 green), I asked, “Are we done with our drawing?” The students responded with, “No! We need to get to 28 apples!”
Before I developed SoE, I would’ve shown the students how to solve this problem using a mathematical equation and then asked them to solve a similar problem using the same type of equation. But regurgitation of a formula without understanding is not math. It doesn’t lead to deeper understanding or future application.
Notice we didn’t start by trying to figure out what the problem was asking. We focused on the relationship between the parts in the story. You may have also noticed the words “in all” in this story. Without comprehension, students would have seen this “keyword” and mindlessly added.
Another Repeated Equal Groups SoE in action
I was asked by a teacher how to use a structure to teach a specific word problem. In this video, I break down how I would go through the process. Notice how I:
- Scaffold and support
- Help them visualize the problem
- Focus on the context
- Use labels
- Discuss what the visuals represent
Modeling stories with SoE might take more time initially, but the investment is well worth the results.
Conclusion
In our journey to help our students become effective word problem solvers, we’ve explored the Parts Equal Total and Repeated Equal Groups structures. By prioritizing understanding over rote procedures, we empower students to experience success with math stories. There is no other reading comprehension tool that helps students internalize word problems.
Although SoE might not be easy to teach, they set our students up for problem solving success. It’s just like establishing your expectations at the beginning of the year. In order to be effective, you have to put the time and energy in up front. Once established, you no longer need to spend excessive amounts of time managing behavior. The investment teaching structures up front will be rewarded at the end.
Next week, we’ll look at how these two structures might work together. Don’t want to miss it? Make sure you subscribe!