There’s a common question that comes up in my work with teachers and students: Is this the right structure?

Here’s why that might not be the question we should ask.

What Are Structures of Equality?

Structures of Equality (SoE) are reading comprehension tools that can be used to model what’s happening in a number story. There are 3 structures – Compare, REG, PET – that can be used to visually represent any word problem type in elementary math. The key to choosing a structure is identifying the math main idea.

Students sometimes use what might seem like the ‘wrong’ structure, a frequent discussion point in professional development (PD). There are scenarios that that tend to drive this conversation:

• Repeated Equal Groups (REG) or Parts Equal Total (PET)?
• REG or Multiplicative Compare?
• Compare or PET?

I talked through examples of REG vs. PET and REG vs. Multiplicative Compare in my last two blogs. Today, we’re going to work through a number story that could lend itself to the Compare or PET structure. 

Before we even begin to think about which structure to use, there’s one thing that’s essential to figure out first: the math main idea. Every number story aligns with one of 3 main ideas.

After students understand how to find the math main idea, they are able to draw a model that accurately represents the situation as it is occurring in the number story. This model doesn’t just represent the problem – it helps students make sense of the mathematics when it’s time to solve.

The problem with typical bar models or other representations is that students can draw them – maybe even accurately – without actually understanding what the problem is asking them to do. With the structures, it’s impossible to draw them without comprehension. Let’s start there.

The Problem with Procedural Strategies Like CUBES

Here’s a typical 2nd grade math problem, taken from North Carolina’s DPI Unpacking Document. It reads: 

Juan has 3 pencils. Brielle has 2 more pencils than Juan. How many pencils does Brielle have?

A traditional approach to this problem would include a procedure such as CUBES (Circle key numbers, Underline the question, Box key words, Evaluate & eliminate, Solve & check). When kids  “pluck out numbers” or “plug and chug”, it’s because they’ve been using a strategy like this, ones that rely heavily on keywords or steps.

Following CUBES often leads to inaccurate models, like the ones shown, because it focuses on keywords instead of comprehension.

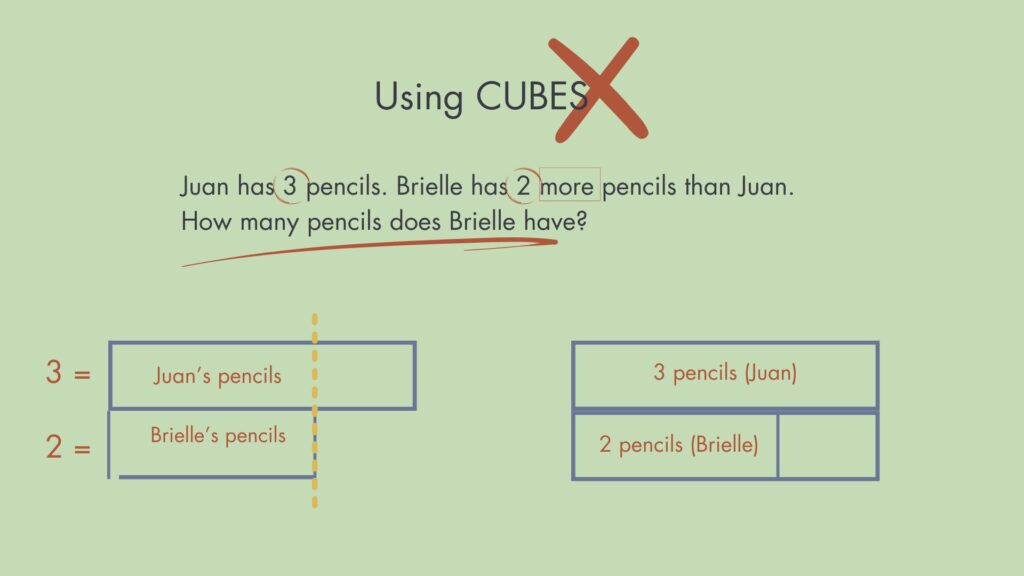
These models are wrong because they don’t represent the situation as it’s occurring in the story. For example, they incorrectly suggest that Juan has more pencils than Brielle. If this model was used to set up an equation, you’d come up with:

• 2 + ___ = 3
• 3 – 2 = ___

Neither of these would lead us to an accurate solution. This problem is not asking us to find a missing part; it’s asking us to compare two distinct sets. Once students have this understanding, they can draw models that will be helpful. 

When Students Choose the ‘Wrong’ Structure

Since the main idea describes comparing two distinct sets, this problem is best represented with a Compare structure (as shown on the left). In this model, we can easily see that Juan and Brielle have the same amount of pencils up to a certain point, the line of equality. We also know the value of the “more”, 2.

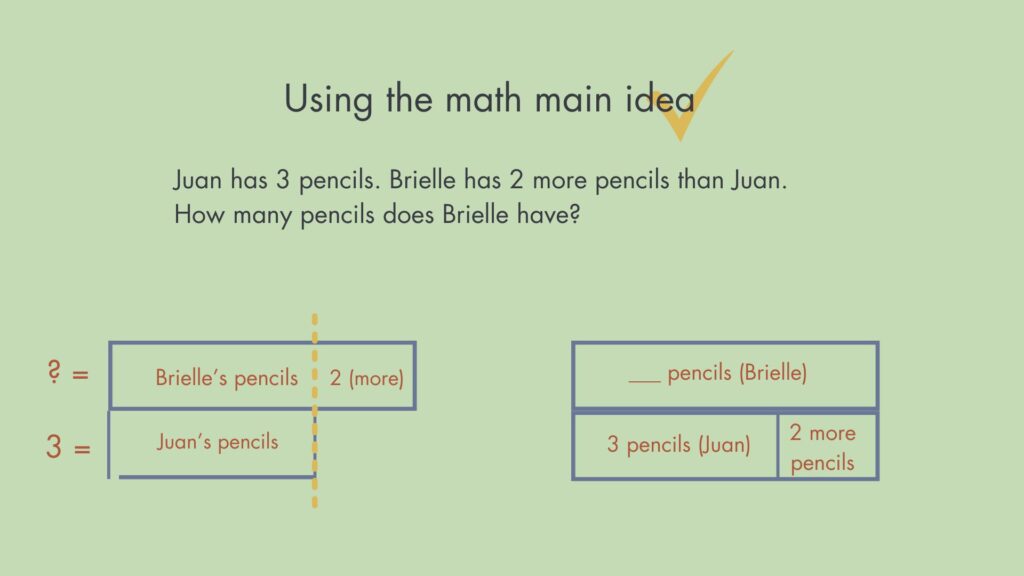
However, you may have a student who draws a PET to represent the same story. This is where the question arises: should we accept this representation?

Some students get stuck in PET because it’s the first one we taught them and they feel comfortable with it. Initially, if a student models this story using a PET and they can explain that the one part represents the difference between the two sets of pencils, you can say something like:

“Oh, I see how your brain is working. Thank you for explaining that to me.” 

Their explanation shows they understand the math main idea. Remember, the point of drawing a SoE is to help students better understand the relationships occurring in the story. It would be impossible for a student to come up with either representation if they didn’t have comprehension.

Why Comprehension Matters More Than the Right Model

At this point, you would continue to emphasize that the math main idea of stories like these describes a comparison relationship. During think-alouds, say things like:

 “When we have a story with this math main idea, we use a Compare structure.” 

As students are working, have them explain their reasoning. If they show comprehension and their model matches what they’re saying, accept it.

Think about it: It’s really amazing when a student thinks mathematically, and can model and justify their thinking. We need to be careful to not inadvertently shut that down by saying, “Nope, wrong SoE.” By valuing students’ reasoning and emphasizing comprehension, we encourage deep mathematical thinking – a skill far more valuable than choosing the ‘correct’ structure.

Ultimately, our goal is to foster comprehension, not just procedural accuracy. When students can explain their reasoning, they’re learning to think like mathematicians.