Understanding Context

Some number stories can be represented by more than one structure, which often raises the question: how do you choose the right one? Accurate math models are a common topic during professional development and my work with teachers. Because teaching is both an art and science, the answer is a bit nuanced.
Let’s explore a problem shared by a teacher in my Facebook group.

The teacher mentioned that she didn’t love the wording of this question, and I agree. While we can sometimes modify our curriculum, other times we have to work with what’s given. Let’s walk through the problem as it’s written.

Here’s the problem:

At a fair, there were three lines with the same number of people in each line waiting to get on the ferris wheel. Which could be the number of people in each line?

The answer choices are:

a. 32

b. 35

c. 37

d. 39

I’d start by asking the same guiding questions I use before modeling any number story. Because students often struggle with reading comprehension, it’s important to ensure they fully understand the context of the problem.

• Who are the characters?
• Where is this story taking place?
• What’s the action occurring?
• Is there a thing being composed or decomposed, or something being compared?

Finding the math main idea

For this problem in particular, students would likely argue that something is being decomposed. Although the value of the total is unknown, the total number of people waiting to ride the ferris wheel is being decomposed into 3 lines.

I’d then ask: What’s the math main idea?

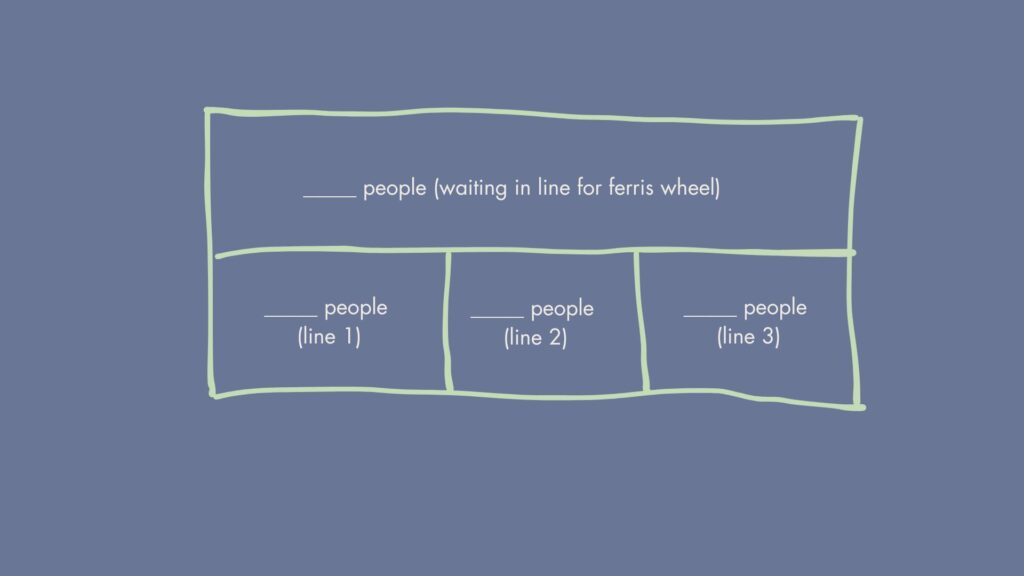
In this case, the math main idea is a total being decomposed into 3 equal groups.

Accurate math models: choosing and discussing structures

Since the groups (or parts) are equal, the most accurate representation is a Repeated Equal Groups (REG) structure, which represents a total being decomposed into equal groups. However, number stories that can be represented by REG can also be represented with a Parts Equal Total (PET) model. That’s because at the heart of the math main idea of these types of stories is composing or decomposing sets.

REG are special because the sets are equal to each other. Therefore, I would accept both a typical REG and a PET structure as an accurate model for this story, especially  if a student could explain how the SoE models the math main idea occurring in the story. 

Our ultimate goal is reading comprehension. I’d follow it up with a question such as: What do we know about the parts? (They’re equal.)

You could even say something like “I noticed some of you drew a PET, while others drew a REG. Both can model the situation. Why is that?”

Connecting the structures and the values

You’ll notice we haven’t addressed the answer choices yet. That’s intentional. We first want students to understand the situation described in the story. Once they can explain their structure, we shift focus to the values.

“We have 4 possible values given: 32, 35, 37, and 39. We don’t know which one is the solution yet. What label in our SoE describes these possible values?” You want to make sure they understand the answer choices represent the total and would be the value next to the label “people waiting for the ferris wheel”. 

While students (and teachers) are still becoming familiar with the structures, the key focus should remain on the math main idea. Over time, students will grow more comfortable with this approach, leading to fewer discussions about which structure is “right”.

Until then, keep focusing your instruction on the math main idea. Model accurate representations by thinking aloud and ask questions like the one above to encourage students to explain their reasoning.

Conclusion

By prioritizing context and modeling clear, accurate representations, we can guide students to see how both a PET and A REG  can model the same story depending on the values and math main idea. Over time, these strategies will become second nature, and discussions will shift from “Which structure is correct?” to “What is the math main idea of this story? What SoE can I use to model that math main idea? and How does this structure help us understand the problem?”