When students approach math problems, especially abstract ones, they often struggle to make sense of the numbers and relationships involved. But what if we could bridge that gap by giving them tools to understand math in a way that feels tangible and meaningful? 

I was excited to come across one of Christina Tondevold’s recent videos, where she shares strategies for deepening comprehension – using real-world contexts and visual models.

These strategies align perfectly with the Structures of Equality (SoE) approach. In this blog, we’ll explore how contextualizing problems, using visuals, and facilitating structured discussions help students engage more deeply with math.

Using Real-World Contexts to Deepen Mathematical Comprehension

In the video above, Christina Tondevold shares a problem sent in by a teacher: 86 is ten less than ?

Out of context, this is pretty confusing, which is why framing math problems within everyday situations can help students relate to mathematical concepts more effectively. For example, here are 3 number stories taken directly from her video, that could also represent the situation occurring in the above problem.

In all of these stories, the math main idea is about comparing two distinct sets. Identifying the math main idea is critical to show that students understand the situation occurring in the story. If students can’t identify the relationship between the numbers, it’s impossible to create a visual representation that helps them make sense of the mathematics.

Once students understand the context, engaging them in discussions further deepens their comprehension.

Structured Conversations Around Number Stories

Like SoE, the video also highlights the importance of engaging students in meaningful discussions about math problems. These conversations help students articulate their thought processes, leading to richer insights and deeper understanding. This approach ensures that students understand the “why” behind their solutions.

Before drawing the models, or even finding the math main idea, it’s helpful to pose questions to kids thinking about what’s happening. This discourages the habit students develop of jumping straight to ‘answer-getting’.

My favorite questions to pose mirror comprehension questions you might ask students when listening to a regular story, but in a math context, such as:

• What is the thing or unit we are counting or comparing?
• What is the story setting?

It’s important to make explicit connections between how we talk about literary stories and number stories.

Visual Models as Tools for Conceptual Understanding

One of the strategies Christina Tondevold emphasizes is the use of visual models. Once students have identified and discussed the math main idea in the stories above, they could represent it with a Compare structure.

If you’re not already familiar with the structures, they are foundationally based upon bar models. But the problem with traditional bar models is that students can draw them without truly comprehending what’s happening in the story.

Once students grasp the relationships in the story, the Compare structure becomes a powerful tool for visualizing the problem. By using values, labels, and the line of equality, the Compare structure ensures that students not only draw the model correctly but also fully understand the mathematical relationships involved.

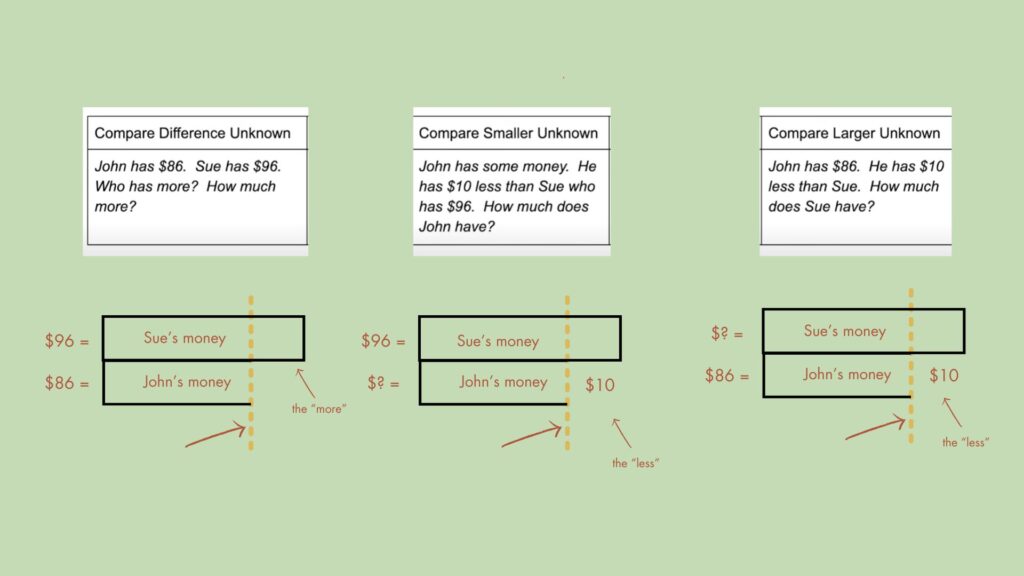
As you can see, the structures look exactly the same, but the unknown value is different based on the situation as it’s written in each number story.

We know problems that require students to compare quantities can be pretty tricky. The deliberate use of visual elements in the Compare structure helps bridge the gap between abstract numbers and their real-world meanings, creating a stronger conceptual foundation.

Conclusion

Helping students make sense of math requires a blend of thoughtful strategies: providing relatable contexts, facilitating meaningful discussions, and guiding students in using visual tools. These approaches encourage students to think critically about the relationships between numbers and develop a deeper understanding of mathematical concepts. 

By shifting the focus away from merely finding the right answer to truly understanding the “why” behind the problem, we can empower students to become confident problem-solvers. Whether through Christina Tondevold’s strategies or Structures of Equality , the goal is the same: making math accessible, engaging, and meaningful for every student.