It’s rewarding when we teach our hearts out and our students get it. As a classroom teacher, I found a lot of pleasure in seeing my students grasp and show mastery of a concept. We celebrate when students get it right, but the real magic happens when they get it wrong.

Why student mistakes matter in math

I believe strongly in the importance of helping students develop a growth mindset. It may seem counterintuitive, but always knowing the answer or what to do actually leads to a fixed mindset. We begin to equate correct with smart. That means, the implication when we get something wrong is that it’s because we’re not smart enough or skilled enough.

This is simply not true. It’s also why I love when students get it ‘wrong’. It presents a massive learning opportunity, one that when navigated well, helps students understand what they do know and how to build from there.

It also creates the opportunity for sense-making, problem-solving, and critical thinking.

The power of ‘wrong’ in math

The article, The Power of Incorrect Answers, states “students must develop the skills required to reason mathematically from kindergarten through grade 12. To bolster students’ ability to prove as well as develop mathematical argumentation skills, create an environment in which students must regularly explain and justify their thinking.”  

As educators, we tend to have students explain their thinking when they’re accurate. I’ve found the real power is in having students explain their thinking when they’re not. 

Uncovering misconceptions: a 3rd-grade example

I define a response as the solution itself and the student work. Let’s start with a seemingly straightforward problem.

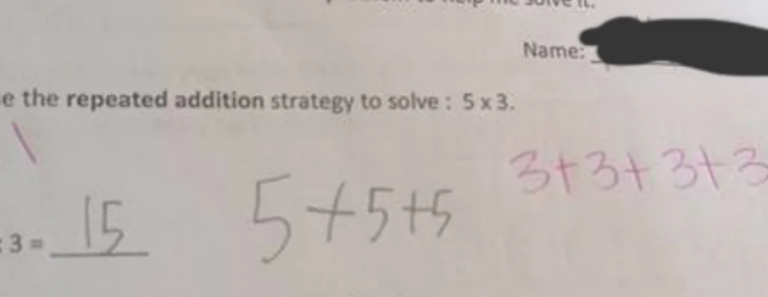
In this case, 15 was an accurate response. But, when working with whole numbers, the multiplication sign can be translated to mean “groups of”. In this case, the expression 5 x 3 means 5 groups of 3. 

It’s also an ideal time to mention the commutative property. 15 was an accurate solution because we know 5 x 3 has the same value as 3 x 5, but they don’t mean the same thing. 5 x 3 = 3 x 5 doesn’t mean they are the same – it means they have the same value.

While this may seem trivial, multiplicative reasoning is the foundation of more complex skills students need later. Without conceptual understanding, they’ll struggle when faced with more challenging problems like fractions or ratios. 

In this example, we can celebrate that this child understands there must be repeated equal groups. We can also infer they have their multiplication facts memorized. This can help us guide our questioning.

We might ask things like “How many groups did you show?” or “How many are in each group?” We could also ask what the expression 5 x 3 means.

Misconceptions give us a starting point for deeper discussions, and by asking probing questions, we can help students rebuild their understanding on a stronger foundation.

The role of misconceptions

Misconceptions are more than just mistakes – they’re windows into a student’s current understanding of a concept. When we uncover a misconception, we’re identifying the gaps in knowledge that need to be filled. This is crucial because misconceptions, if left unaddressed, often compound over time, making it harder for students to grasp more complex mathematical ideas later on.

Building on student knowledge

Let’s take a look at an example 4th grade problem.

In the example below, the solution is accurate. If the student hadn’t shown any work and drawn a Parts Equal Total model, we wouldn’t even realize they might have misconceptions.

Once we do, our first inclination might be to look at the errors made in the student work sample below. My challenge to you is to first look to uncover what they do know.

This student knows:

• the unit is 8ths
• the unknown value is a part 

Now let’s look at what they struggled with:

• They didn’t realize the whole (or total) was 6/8 not 8/8. 
• They put 6/8 as a part when it should have been a total.
• They didn’t notice they didn’t use 4/8.
• There were no labels.

Based on these observations, we can engage in a rigorous discussion that will help move this student’s thinking forward. 

Encouraging deeper thinking

Here are possible questions to pose or feedback to give: 

• What does each of your values represent? How could they be labeled?
• What happened at the beginning of this story? Where is that in your structure?
• Remind me of the action happening in the story. Where is that represented in your structure?

Conclusion

In the classroom, mistakes aren’t something to shy away from. They’re an invaluable tool for helping students develop a growth mindset and deeper understanding. When students explain their thinking, even (and especially) when they’re wrong, it opens the door to critical problem-solving skills and sense-making that memorization alone can’t provide.

By asking thoughtful questions and guiding students through their misconceptions, we help them uncover the building blocks of mathematical reasoning that lead to long-term mastery. So, the next time your students get it wrong, remember – it’s an opportunity for growth.