Addition Doesn’t Always Mean Bigger. Subtraction Doesn’t Always Mean Smaller.

We recently explored why subtraction doesn’t always mean take away. Before that, we dug into how equal doesn’t mean the same as. This post builds on both. 

Today, we’re talking about another message we often give students, without realizing it’s going to cause problems later. We say:

• “When you add, your number gets bigger.”
• “When you subtract, your number gets smaller.”

The problem is, this isn’t always true. We actually run into this in kindergarten, as soon as we introduce the number zero.

If I have 6 blocks and add zero, I still have 6. If I have 6 blocks and subtract zero, I still have 6. In both cases, we’re performing an operation, but the value of the original number doesn’t change.

That can be surprising for students who’ve already learned “adding means more” and “subtracting means less.”

Instead of saying “adding always makes it bigger,” we can say something like: “Usually when we add, the number gets bigger. But not always. Let’s see what happens.”

It’s still developmentally appropriate. It still supports their growing number sense. And it starts building a foundation for math that makes sense, even when it gets more complex.

This idea that “adding means more” and “subtracting means less” feels true because it usually is, especially if you’re only working with whole numbers. Adding often increases the value. And subtracting often looks like you’re making something smaller.

If I have 3 apples and I get 4 more, I now have 7. Bigger.
If I have 10 blocks and take away 6, I have 4. Smaller.

Those examples are helpful when kids are first learning how to join and separate sets. But if we present those ideas as always true, we’re setting kids up for confusion later.

Where misconceptions begin

When kids hear “addition makes numbers bigger,” they believe that’s what addition means. Later, when they encounter other kinds of numbers, they’re surprised when that rule doesn’t hold. Instead of realizing the context has changed, they assume they’ve done something wrong.

Let’s take a look:

Negative numbers:
If you add –3 and –11, you get –14.
That’s smaller than either of the numbers you started with.

Subtracting negatives:
If you take –11 and subtract –5, you get –6.
That’s actually greater than –11.

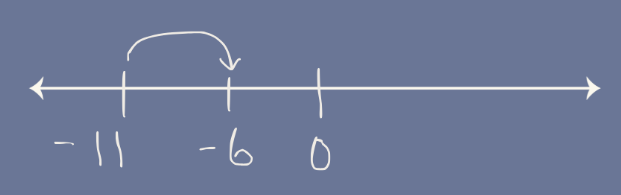
Addition didn’t make the number bigger. Subtraction didn’t make it smaller.

When we define addition as “makes things bigger,” students start thinking:

• All addition is about increase.
• The sum is always greater than the parts.
• Subtraction will always give you less.

We unintentionally teach them to expect math to follow rules that aren’t universal. So when math stops matching those rules, they lose trust in the process or in themselves. They start to see math as procedural, rather than something to make sense of. 

This is all part of the same bigger idea: We often teach language that works in one context, and kids assume it works in all of them.

And when the language stops matching the math…

They try to force it. We’ve all heard kids say “You can’t take 8 from 5” because they haven’t yet learned about different types of numbers. They see 6 = 2 + 4 and say, “That’s not right; it’s backwards!”

“The main cause of errors and misconceptions is superficial understanding… students resorted to memorizing rules because of surface understanding.”
—Khalid & Embong (2020)

In other words: when we oversimplify, kids don’t question us. They memorize. And when the pattern doesn’t hold, they freeze. They’ve learned that math is about following steps, not making sense of relationships. That the goal is to remember the trick, not understand the concept.

So how do we teach this better?

Instead of focusing on what happens to the number, we should focus on what’s happening in the relationship.

For example, depending on the context, you might say:

• “Addition means combining quantities or composing parts to form a total.”
• “Subtraction means finding the difference between two values, or how far apart they are on the number line.”

This kind of language still works when students eventually encounter fractions, decimals, and other kinds of numbers. It’s accurate now, and it leaves room for the bigger picture later.

Instead of: “When you add, the number gets bigger.”

Try giving them precise language such as:

“When we’re working with whole numbers, adding does end up in a bigger number. But that’s not always the case with other kinds of numbers, and you’ll learn about those later.”

Here’s another example of how this might sound, depending on the context:

“Sometimes subtraction means taking something away. Let’s see if that’s the case here.”

This keeps the language true while building flexibility.

Final thought

A lot of things in math are true until they’re not.

That’s why we have to be careful about the stories we tell, especially to young learners. If we want students to understand math deeply, we can’t build that understanding on rules that only work some of the time.

If you’ve told students “addition makes numbers bigger” before, you’re not wrong. It’s often true. But now you know there’s a more precise way to say it. One that grows with them instead of boxing them in.

Just like we did with “take away” and “equal,” we can shift how we talk about addition and subtraction, without overwhelming kids. Because math makes sense. And our language should help students see that.