It’s not an alligator mouth. And Pac-Man isn’t chasing any ghosts. 

Cute should never take the place of conceptual understanding. Greater than and less than are complex ideas, and while these “tricks” may be well-intended, they’re not helpful.

An educator in my Facebook group recently asked an important question around when to introduce the greater than and less than symbols. That question inspired this blog. I’ll answer her question and also dig into:

• Why we need to start with understanding, not symbols
  
• What kids need to be able to say before they’re ready to write
  
• How to scaffold comparison work with integrity
  
• What to do when your curriculum jumps ahead
  

When Should the Greater Than and Less Than Symbols Be Introduced?

My answer may not be as straightforward as you’d like, but here it is: Symbols should be introduced when students are ready.

That means they:

• Have a conceptual understanding of the mathematical idea you’re introducing
  
• Can verbalize that understanding with clarity
  

It’s not realistic to expect all of your students to hit that readiness point at the same time. But what is realistic, and essential, is that we’re intentional in how we lay the groundwork. We model. We listen. We adapt. We don’t rush to symbolic representation just because it’s next in the pacing guide.

Here’s the original question from the Facebook group and how I responded:

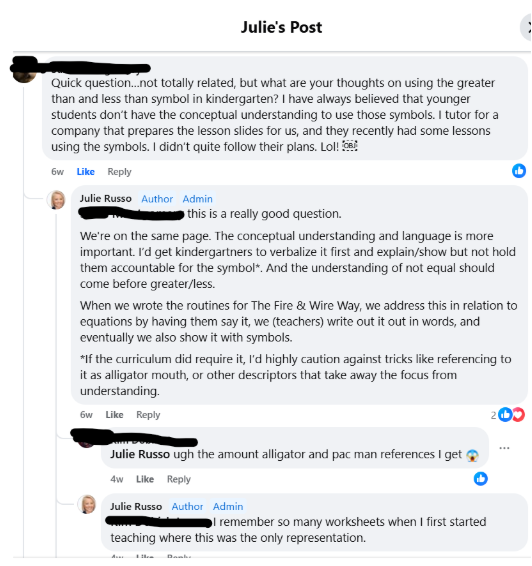
Symbols Don’t Drive Understanding. They Record It.

Math symbols are just ways to represent thinking. They are not the thinking itself.

Students need to make sense of ideas before we hand them the shorthand. When we jump to symbols too early, we force kids to operate in a language they don’t yet speak fluently, and it shows. We get random guesses, flipped symbols, and confusion that’s chalked up to “careless mistakes” when the issue is actually conceptual.

Verbal First. Always.

If a student can’t say it, they’re not ready to write it. That’s a good rule of thumb, especially for comparison work. We want to hear students say things like:

• “Eight is greater than six because it’s farther from zero on the number line.”
  
• “Four is less than seven because seven has more ones.”
  
• “These are not equal because one group has more.”
  

When we hear those explanations, we know we’ve got something solid to build on. That’s when we can start saying, “We can also write that like this…” and show how the symbol captures what they just said.

This isn’t just my opinion. It’s supported by professional organizations and research. The National Council of Teachers of Mathematics (NCTM) highlights that reasoning and sense making are foundational to mathematical proficiency—and when we skip over those steps, students struggle and disengage. Verbal reasoning builds a bridge to symbol use. 

Build the Right Sequence: Equal → Not Equal → Greater/Less

We’ve seen over and over that kids who struggle with comparison symbols often don’t have a firm grasp of equality. That’s where the real work starts.

Start by helping students understand that an equal sign means both sides have the same value. Then introduce not equal, a concept that pushes them to compare without yet putting in order by size or value. Once that’s solid, they’re ready to explore which is greater and which is less.

Visuals are key here:

• Show it on number lines
  
• Use ten frames
  
• Model with manipulatives
  
• Talk about it a lot
  

These tools help students see what the symbols will later represent.

Introducing Symbols: What It Looks Like When They’re Ready

When students are confidently using language to describe comparisons, that’s your cue. Here’s how that might look:

• Student: “Nine is more than five.”
  
• You: “Yes! That’s right. Nine is more than five. We can also write it like this: 9 > 5.”
  
• Then model it. Talk through it. Let them match statements to symbols with support.
  

Don’t assume that just because they can say it once, they’re fluent. Keep it visual, keep it verbal, and give them lots of chances to connect ideas to symbols in context.

What If My Curriculum Introduces It Before My Kids Are Ready?

You’re not alone if your materials introduce comparison symbols before kids are ready. Here’s what I’d recommend:

• Still prioritize the talk. Let students say the comparisons, and don’t rush symbolic mastery.
  
• Use the symbols as a teacher modeling tool, not a student accountability tool.
  
• Focus your assessments on understanding, not just correctness of symbol use.
  
• Advocate when you can, but adapt with integrity when you can’t.
  

And if you’re looking for ways to do that kind of adapting with thoughtfulness and fidelity, Graham Fletcher shares helpful insights in this conversation about the role of progressions in instruction. When we understand what comes before and after a skill, we’re better equipped to make those in-the-moment decisions without compromising student understanding.

Teach the Math, Not the Shortcut

This is one of those spots where we have to protect our teaching. It’s easy to get swept up in the push to move quickly, but we’re here to build thinkers—not trick users.

We don’t need to dress up inequality with alligator mouths or cartoons. We need to slow down, give students real models, real language, and real opportunities to understand.

So the next time you see a lesson jump to symbols, pause and ask: Do my students understand the ideas these symbols are meant to represent? If not, it’s okay to press pause. Understanding is worth the wait.

What’s Next?

If you’re looking for a way to build these ideas into your daily practice without adding one more thing to your plate, check out my book, The Fire & Wire Way. It’s a collection of daily routines designed to be quick, simple to implement, and deeply impactful.

Two of the foundational ideas woven throughout the routines are comparisons and equality—the very concepts that support meaningful use of symbols like greater than and less than. The routines systematically and explicitly build these understandings while also nurturing critical number sense skills across the board.