Choosing which structure best represents the math main idea of a number story is not always straightforward. The biggest problem most teachers face is their students don’t understand what word problems are asking them to do. It’s a comprehension issue. And it’s particularly challenging with multiplicative comparisons.

This is why Structures of Equality (SoE) is a better visual representation than a typical bar model. It’s impossible for students to draw the structures without comprehension of what’s occurring in the story. They must be able to identify the math main idea.

As the mathematics gets more complex, figuring out the math main idea does too. This leads to conversations over which is a more accurate visual representation: 

• Repeated Equal Groups (REG) or Parts Equal Total (PET)?
• REG or Multiplicative Compare?
• Compare or PET?

Let’s tackle the “REG or Multiplicative Compare?” debate through a question a teacher posed in my FB group.

If you’re new to SoE, you can learn more about the structures here.

Today we’re going to focus on REG and Multiplicative Compare. REG is helpful when the math main idea describes composing equal groups or parts to form a total OR decomposing a total into equal groups or parts. We use the Multiplicative Compare model when the math main idea describes multiplicatively comparing two distinct sets.

Here’s the question that was submitted by a teacher.

The number story reads: Parker has twice as many cars as Luke. Together they have 39 cars. How many cars does Peter have?

This can be a tricky question, whether you’re new to SoE or not. The first thing you have to do is determine the math main idea. In this case, the main idea describes comparing two distinct sets with each set composed of equal parts, which lends itself to the Multiplicative Compare model. We’re comparing Parker’s sets of cars to Luke’s set of cars.

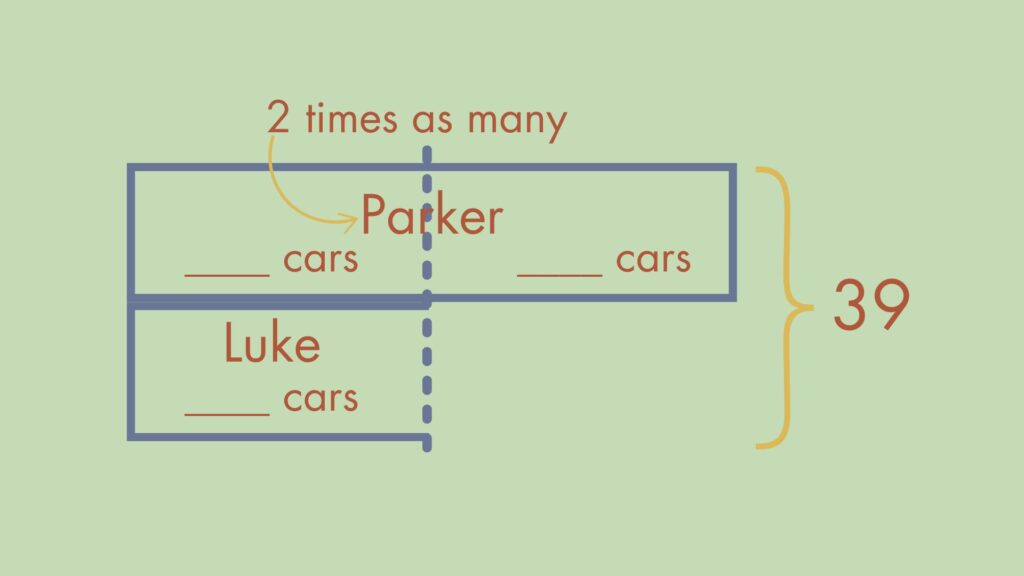
Parker has twice as many cars as Luke, so the bar that represents his cars is twice as long as the bar that represents Luke’s cars. The line of equality (the dotted line) helps us see the point up to which they both have the same amount of cars. We know there are 39 cars total. 

Once students understand what the problem is asking, they have the flexibility to use whatever strategies are most efficient for them when it comes time to solve. They have multiple access points to the same problem, which is part of the beauty of SoE.

That same idea applies to students who might argue this problem should be represented with a REG structure. As long as they can justify their thinking in a way that makes sense, I would accept an REG model (as shown below). We have to meet kids where they are in their understanding.

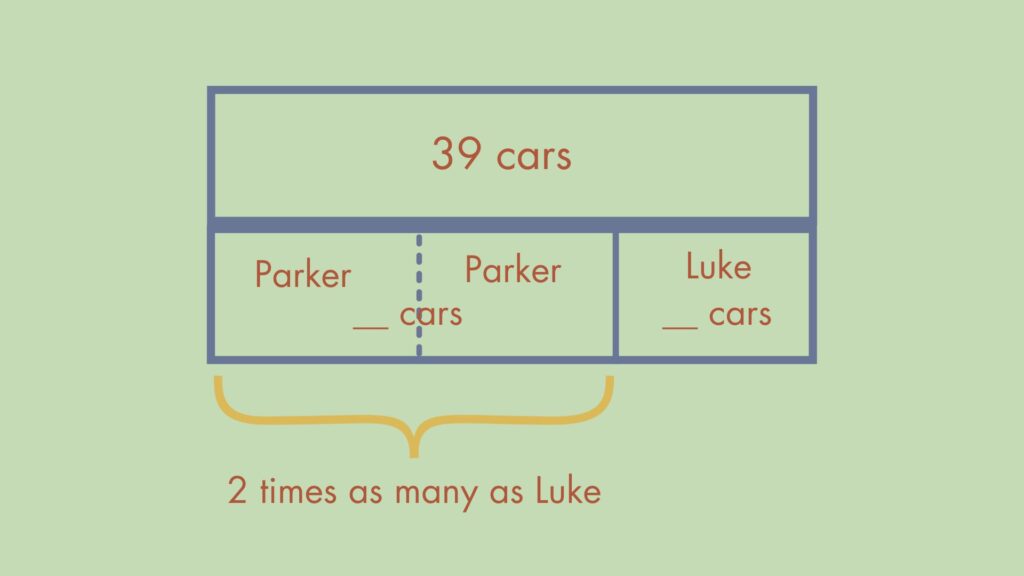
This student understands we are comparing the amount of cars Parker has to the amount of cars Luke has, which means they grasp the math main idea. Even though they represented it with a REG, they’re not arguing that the story is about composing groups or decomposing a total. Not only can we accept this model, we can celebrate the application of their conceptual understanding. Remember, the goal here is comprehension. 

Think about it: wouldn’t it be pretty cool if a student was so invested in their work they wanted to argue for their model. Isn’t that what we strive for – proficient mathematicians who think critically and construct viable arguments?

So, yes, the stronger model for this particular problem is a Multiplicative Compare model. But as long as your students can articulate the math main idea of the number story and why their visual is a representation of that idea, they’ve demonstrated exactly what you want: understanding of what’s happening in the problem.