In math, we tend to think of units as something we talk about when we’re teaching measurement. But we don’t always think “Why are units important in math?” Today, I want to explore why they’re a critical part of comprehending word problems, or number stories.

It’s been awhile since we’ve had a refresher on the 3 components of Structures of Equality (SoE), so let’s start there. 

A SoE is made of three crucial elements. They MUST:

• Contain values (numbers)
• Have labels (units of measure, the things you are counting…)
• Represent equality

When a student includes all three, it indicates comprehension.
▶️ If you’re new here, I encourage you to take a peek at one of my previous blogs where I give you a basic overview of what SoE are and how they came to be.

Why are labels a crucial element of every structure?

Labels help us identify the thing we are counting. They help us categorize quantities and put them in context. Being able to conceptually understand what is happening in number stories is the key to students being able to successfully solve them.

Labels are also one of the key components that differentiate bar models from SoE. It’s possible for students to draw a bar model without a complete understanding of what a number story is asking. But it’s impossible to visually represent a number story using a Structure of Equality unless you have comprehension. Let’s take a look using the example below.

How labels help students comprehend – a bar model vs SoE comparison

The example number story:

There are 29 students on the playground. Some more students show up. There are now 47 students. 

Notice there’s no question posed. We’ll come back to that.

At first glance, it seems like both representations could be drawn by a student who understands:

• The total number of students is 47. 
• We know a part of the total – 29.
• We’re trying to figure out the unknown part.

But in the bar model, these are just numerals. We don’t know what part of the story they represent. And it’s entirely possible that a student could have plucked out the “big number” and put it in the big bar without understanding that it represents the groups of students combined. They would solve and get an accurate answer. And we would have no idea that they didn’t comprehend what the problem was asking.

This is why so many teachers I’ve worked with over the years get frustrated with number stories. It seems like their students understand them, but when it comes time to solve them independently they get frustrated and give up.

Now let’s think of a few questions that could be posed for this problem:

• How many students showed up on the playground?
• How many more students were on the playground than the number of students that showed up?
• If the students that were originally on the playground went back to class, how many students would be left?

With our Parts Equal Total structure, a student could easily tackle any of these questions because they have a clear understanding of what each value represents. In order to label them correctly, students have to understand the context of what’s happening in the problem. 

But do the labels really matter?

You might be thinking that if  students can solve correctly without the extra work of labels, are they really that important? I’d answer that with a resounding yes!

Math is about more than ‘answer getting’. It’s about critical thinking and problem solving. Solving a number story without understanding the context is like reading a storybook without comprehending what’s happening. For students to become proficient mathematicians (and readers), comprehension is a key piece of the puzzle. 

Notice the level of details in the labels below. If a student can draw a visual representation like this, we know they understand what each value in the number story means. You could even add (on the playground now) to the label in the total bar. When it comes time to write equations to match number stories, they’ll have the flexibility in thinking to successfully represent this story symbolically, regardless of the question posed.

What’s the connection between labels and units?

A label is the way we name a unit. It makes sense that we need to include the labels for our units when we study measurement. 237 inches is very different from 237 yards. Units give us the context to visualize the value of these numerals.

You might be wondering how that applies to number stories. Let’s talk first about how it impacts students at the elementary level. Then, we’ll talk about how it sets them up for success across multiple levels and strands of mathematics.

Units in number stories at the elementary level

In our example above, the label “students” might not seem important. If each part and the total represents students, why would we need to write it out? In addition to the ideas mentioned above, let’s think about a similar number story. 

There are 29 cats at the shelter. Some dogs show up. There are now 47 animals.

The structure of the story is the same. So are the values. But the context is completely different. Rather than having the same unit throughout the problem, we’re thinking about cats, dogs, and animals. The label for each value represents a different character in our story.

I love the way Dr. Valerie Faulkner described this during a training I attended with her. “Let’s say you have 3 turtles and 5 ducks. If you were to add them together, what would you end up with? Terducks?! Duckurtles?! That doesn’t even make sense! In order to compose these parts to form a total, we have to think about what they have in common. They’re both animals. The unit matters.” 

Now let’s think about what happens when we get into number stories that require the use of multiplicative thinking. Both whole number multiplication and division require us to think about a total, a number of groups, and the number in each group. To understand and solve number stories, we need to understand what each value represents. 

As we begin to work with fractions (and then decimals and so on), these problems become more about scaling. Students are now thinking about multiplicative relationships in a different way. If they don’t understand what the values represent, they won’t be able to visualize what’s happening in the problem and likely won’t be able to conceptualize it.
It’s the context that tells us what these problems really mean. Christina Tondevold gives an excellent example of this in the “context matters” part of “Does multiplication mean ‘groups of’”?

How labeling units helps lay the foundation for fractions

If you’ve ever taught students in third grade or above, you’ve likely seen the “deer in headlights look” they get when fractions appear. Especially in number stories! They’ve worked with whole numbers for so long that fractions seem like a foreign language.

One of the first concepts we introduce when we teach fractions is the idea of the unit fraction. Sometimes this is defined as a fraction with a 1 in the numerator. While it’s true that unit fractions fit this description, the meaning of a unit fraction is a lot more complicated than that.

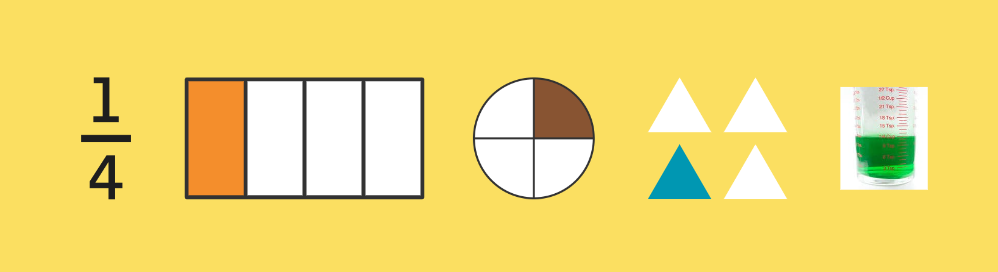
These are all examples of ¼. But what do they mean? To think about the unit fraction, we have to consider the denominator. Derived from the Latin word “nomen”, denominator means “to name”. It literally names our unit. 

In this case, our denominator is 4, which means our whole has been partitioned into four equal parts. That part is now our unit, which means one of those four parts is our unit fraction. Just like we counted by students or animals, we are counting in fourths.

Thinking about ‘terducks’ and ‘duckurtles’ can help us understand the importance of units when it comes to operations with fractions. Whether it’s a number story or a symbolic equation, you need to know what each value means.

For example, let’s consider ⅔ + ¼.

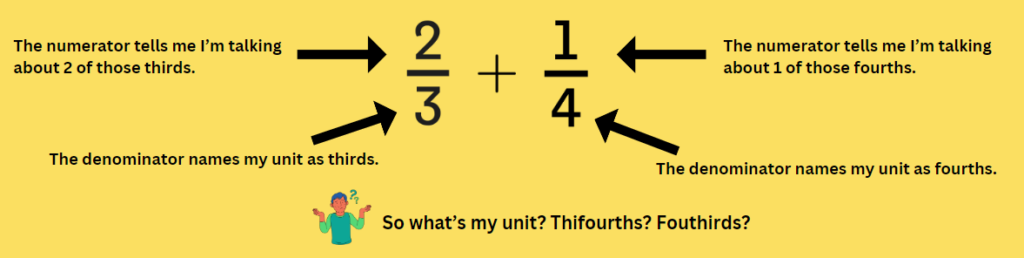
If students have been taught to think procedurally about math, they can find the value of this expression. But that doesn’t mean they understand it. 

If students have been taught conceptually, they understand the idea of the unit fraction. They know:

• ⅔ has the same value as ⅓ + ⅓.
• Thirds and fourths are different units (just like turtles and ducks). 
• In order to make sense of this problem, we have to find a common way to name or label our unit (a common denominator).

Teaching students to label their units in the context of number stories allows them to think critically about abstract concepts, such as finding a common denominator. If you want to explore more about how units play an important role in fractions, check out the examples in “Why the unit of measure matters”.

When you start to think about all the ways the understanding of units plays into mathematics, it’s actually pretty amazing.

Units and labels beyond number stories and fractions

The understanding of units is one of the most foundational concepts in math. In a quick brainstorming session, here are just a few ideas I came up with:

• Labeling the x and y coordinates to understand the relationship between dependent and independent variables
• Unit rate 
• Operations with decimals
• Powers of ten
• Proportional relationships

(Maybe I’ll explore these in a future article!)

Conclusion

Building conceptual understanding of units in early math is one of the most fundamental skills we can provide for our students. It not only plays an important role in comprehending and solving number stories, but in all facets of mathematics. 

Now that you’ve seen the opportunities you have to set a strong foundation, here’s the next step I’d encourage you to take: Even if you’re not using SoE yet, ask your students to label the values in their equations every time. It might surprise you to see how it deepens their level of understanding. I like to ask, “What’s the thing we’re counting?” Give it a try and let me know how it goes!

You can find more tips and get access to exclusive freebies in my weekly emails. Haven’t subscribed yet?

<!– End Constant Contact Inline Form Code →