January 6, 2024
You’ve had an introduction to PET and seen a few students in action. You’ve also seen how it relates to specific CGI problem types and watched video breakdowns on how to teach PET.
Today we’re going to do a deeper dive. We’ll explore:
- sample 1st, 2nd, & 3rd grade story problems
- How they relate to CGI
- How the PET structure relates to the standards
- The gaps filled by Structures of Equality (SoE)
How to introduce a number story
Structures of Equality (SoE) aren’t procedures. There’s not a specific step-by-step process to follow. But there are key teacher moves you need to make every time. Before we narrow our focus to Parts Equal Total, let’s start with the big picture.
I created SoE because I noticed the problem with word problems isn’t the computation. It’s the comprehension. Students don’t understand what is happening in the context of the story. I knew that developing a reading comprehension tool would solve the problem.
But before you use any structure to visually represent a number story, you have to start with an in-depth discussion.
Here are a few of my go-to story element questions:
- What do you notice?
- What’s happening in the story?
- What’s the setting?
- Who are the characters?
- What’s the action? (What’s the verb?)
- What’s the math main idea?
- What’s the thing we’re counting?
- Close your eyes and visualize the story. Have you ever had (item)?
- What’s a (item)?
Once students have an understanding of the context, you’re ready to think about how to represent it with a structure. There are 3 structures and they can be used to represent any problem in the K-5 NC Standard Course of Study (which correlates very closely with Common Core standards). Today, we’ll explore one of them.
What does it look like to model a problem with a Parts Equal Total (PET) structure?
A student can use a Parts Equal Total SoE when a math story describes composing 2 or more parts to form a total. Or when a math story describes decomposing a total into 2 or more parts. Drawing a PET SoE helps students understand the relationship between the parts and the total.
I’m sharing two videos I created showing you how to teach number stories, each with a missing part. Pay attention to the introduction of each story problem and how it helps students understand the relationships between the values in the problem.
? Stickers
Did you notice how the question itself wasn’t even an important part of the discussion? There’s no need to use tricks like “underline the question” when students have comprehension.
How PET structures compare with Cognitively Guided Instruction (CGI)
One of the things I appreciate about CGI is that it considers the situations in story problems. There’s an emphasis on comprehension and the relationships within the problems. But it’s overwhelming and complicated. And there’s often a focus on creating the equation before visually representing the story.
There are 8 CGI problem types that can be represented with a single structure, PET. This allows students to focus on the relationships and create a visual representation before they worry about symbolic representations.

How does PET support understanding of 1st-grade word problems?
In the 1st-grade standards, students are expected to write equations to match story problems.
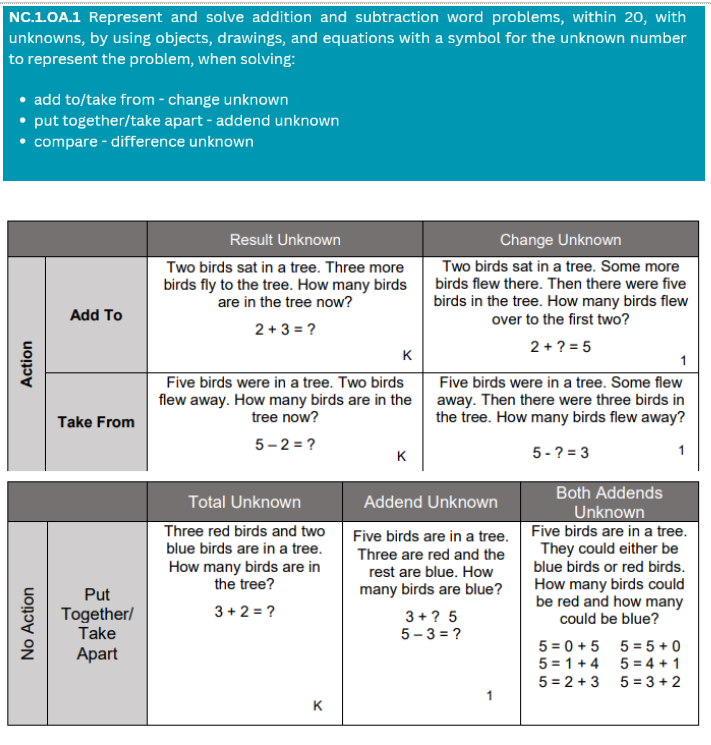
Having 4 different problem types to choose from can be confusing. It also tends to lead to work that students can engage in without truly understanding the problem.
For example, with an add to/result unknown problem, students might pick the first number, write it down, pick the second number, write it down, and then add them together because that’s what the problem type calls for. However, they can do this without having comprehension.
While they can draw a bar model, they don’t have to. Students often go straight to a strategy and finding a solution. It appears they have understanding but that’s not always the case. I used to get so frustrated when I thought my students knew how to tackle word problems but then couldn’t do it independently.
With a PET structure, students understand that there are parts. The parts are equal to the total. Each part or total is represented by a value within the problem. Students have to understand the relationship between the parts in order to draw the representation correctly. They internalize this and can apply it to other problems that require composing parts or decomposing a total. They can then easily write the matching equation and solve it with a strategy of their choice.
How does PET support understanding of 2nd-grade word problems?
In the 2nd-grade standards, students begin to work with larger numbers and two-step story problems. They also represent unknown values with symbols.

Let’s talk about the two-step word problems. With SoE, these are simplified.
Consider the marbles problem (two operations, same). Instead of thinking about the story problem as having two steps, students only have to consider the relationships within the problem. They recognize that there are 3 parts. And they know those parts will be equal to the total. They can then use their visual representation to create an equation and solve.
Now let’s consider the peas problems (two operations, opposite). This is a bit more complicated so I made a quick video for you. I didn’t include the labels and values and talk about equality for these purposes. When you’re working with students, you ALWAYS want to include those elements. This is so you can see what the PET structure could look like for this type of problem.
There are 9 peas on the plate. Carlos ate 5 peas. Mother put 7 more peas on the plate. How many peas are on the plate now?
? Peas
How does PET support understanding of 3rd-grade word problems?

In the 3rd-grade standards, students tackle two-step problems with unknown values in any position and represent the unknown with a letter.
Because the standard doesn’t call for a visual representation, students are commonly taught to write an equation without creating a model. By skipping this step, it’s difficult for students and teachers to understand where the comprehension breakdowns occur for students who are struggling.
Consider this problem from the NC 3rd grade unpacking document:
The bagel shop has 79 plain bagels, 87 cinnamon raisin bagels and some blueberry bagels. There are a total of 241 bagels. Write an equation to find the total number of blueberry bagels. Show your work and find the answer.
Students who lack comprehension will “plug and chug”. They’ll pick out numbers and an operation. Since it asks them to write an equation to find the total number of blueberry bagels, they’ll likely come up with 79 + 87 + 241 = b.
If they have been working with the PET SoE, they will know exactly how to approach these problems because they’ll understand what is happening within the context of the story.
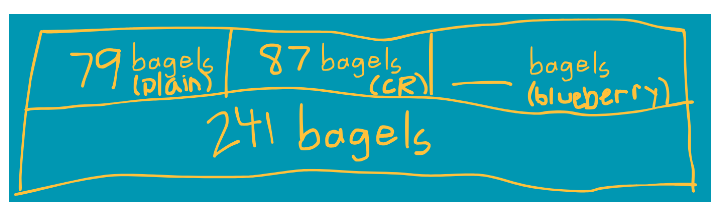
They can then write multiple equations that represent the situation:
- 79 + 87 + b = 241
- 241 – 79 – 87 = b
Conclusion
Parts Equal Total, like all SoE, is a reading comprehension tool. When students use the PET structure to visually represent what is happening in story problems, they’re able to demonstrate an understanding of any of the problem types shown above. It provides a consistent framework for students to comprehend. They can see explicit connections as they progress through grade levels.
Rather than focusing on problem types and equations, students notice the relationship between the values in the problem. When they model these with a structure, they demonstrate true understanding.
While SoEs are simple, they’re not easy to implement initially. In my weekly emails, I include actionable tips and free resources. Not on my list yet?
Resources:
NC Department of Public Education. (2022, June). 1st Grade Mathematics Unpacked Content. https://www.dpi.nc.gov/nc-1st-grade-math-unpacking-rev-june-2022/open
NC Department of Public Education. (2022, June). 2nd Grade Mathematics Unpacked Content.https://www.dpi.nc.gov/nc-2nd-grade-math-unpacking-rev-june-2022/open
NC Department of Public Education. (2022, June). 3rd Grade Mathematics Unpacked Content. https://www.dpi.nc.gov/nc-3rd-grade-math-unpacking-rev-june-2022/open